The value of a coin varies to the square of its radius, when its thickness is constant. The radius of a coin is 1.5 cm and its value is Rs. 2. What will be radius of a coin if its value is Rs 5?
The correct Answer is:2.4 cm
To solve the problem, we need to use the relationship between the value of the coin and the square of its radius. Here’s a step-by-step solution:
Step 1: Understand the relationship
The value V of the coin varies with the square of its radius r. This can be expressed mathematically as:
V∝r2
This means that:
V=k⋅r2
where k is a constant of proportionality.
Step 2: Find the constant k
We know that when the radius r=1.5 cm, the value V=2 Rs. We can use this information to find k:
2=k⋅(1.5)2
Calculating (1.5)2:
(1.5)2=2.25
Now substituting back into the equation:
2=k⋅2.25
To find k, divide both sides by 2.25:
k=22.25=89
Step 3: Set up the equation for the new value
Now we need to find the radius r when the value V=5 Rs. Using the formula:
V=k⋅r2
Substituting the known values:
5=89⋅r2
Step 4: Solve for r2
To isolate r2, multiply both sides by 98:
r2=5⋅98
Calculating the right side:
r2=458
Step 5: Find r
Now, take the square root of both sides to find r:
r=√458
This can be simplified:
r=√45√8=3√52√2
Rationalizing the denominator:
r=3√104
Step 6: Approximate the value of r
To get a numerical approximation:
√10≈3.162
Thus:
r≈3⋅3.1624≈9.4864≈2.372 cm
Final Answer
The radius of the coin when its value is Rs. 5 is approximately 2.37 cm.
---
The value V of the coin varies with the square of its radius r. This can be expressed mathematically as:
V∝r2
This means that:
V=k⋅r2
where k is a constant of proportionality.
We know that when the radius r=1.5 cm, the value V=2 Rs. We can use this information to find k:
2=k⋅(1.5)2
Calculating (1.5)2:
(1.5)2=2.25
Now substituting back into the equation:
2=k⋅2.25
To find k, divide both sides by 2.25:
k=22.25=89
Now we need to find the radius r when the value V=5 Rs. Using the formula:
V=k⋅r2
Substituting the known values:
5=89⋅r2
To isolate r2, multiply both sides by 98:
r2=5⋅98
Calculating the right side:
r2=458
Now, take the square root of both sides to find r:
r=√458
This can be simplified:
r=√45√8=3√52√2
Rationalizing the denominator:
r=3√104
To get a numerical approximation:
√10≈3.162
Thus:
r≈3⋅3.1624≈9.4864≈2.372 cm
The radius of the coin when its value is Rs. 5 is approximately 2.37 cm.
Topper's Solved these Questions
- RATIO, PROPORTION & VARIATIONBook:ARIHANT SSCChapter:RATIO, PROPORTION & VARIATIONExercise:INTRODUCTORY EXERCISE - 4.1
Explore 12 Videos
- RATIO, PROPORTION & VARIATIONBook:ARIHANT SSCChapter:RATIO, PROPORTION & VARIATIONExercise:INTRODUCTORY EXERCISE - 4.2
Explore 5 Videos
- RATIO AND PROPORTIONBook:ARIHANT SSCChapter:RATIO AND PROPORTIONExercise:HIGHER SKILL LEVEL QUESTIONS
Explore 21 Videos
- SEQUENCE, SERIES & PROGRESSIONSBook:ARIHANT SSCChapter:SEQUENCE, SERIES & PROGRESSIONSExercise:Final Round
Explore 18 Videos
Similar Questions
The value of a coin varies directly to the square of its radius, when its thickness is constant. The radius of a coin is 1.5 cm and its value is ₹ 2. What will be the radius of a coin if its value is ₹ 5?
View SolutionThe area of a circle (A) varies directly as the square of its radius. The area of the circle of radius 7 cm is 154 cm2. What is the area of the circle of radius 35 cm?
View Solution
Knowledge Check
The area of a circle is 346.5 cm2. Find its radius (in cm).
A10.5B21C7.5D15The radius of a cylinder is increasing at the rate of 5cm−1min, so that its volume is constant. When its radius is 5 cm and height is 3 cm, then the rate of decreasing of its height is
A6cm−1minB3cm−1minC4cm−1minD5cm−1minIf the density of a planet is constant, then the curve between value of g on its surface and its radius r will be-
A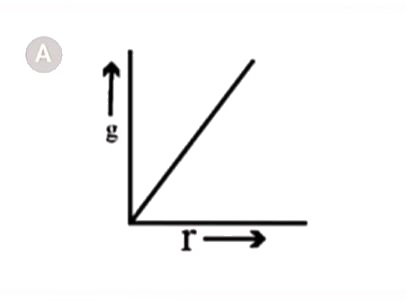 B
B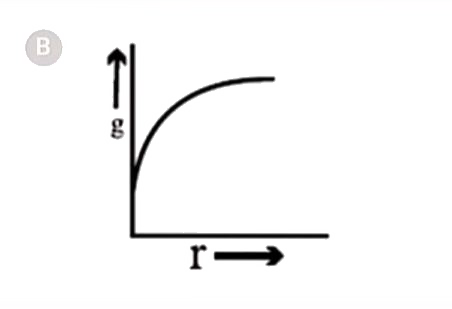 C
C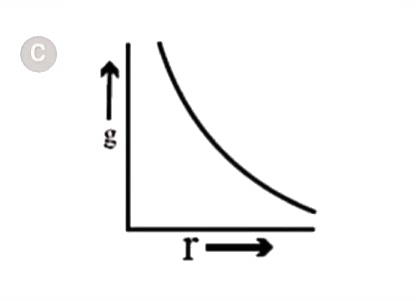 D
D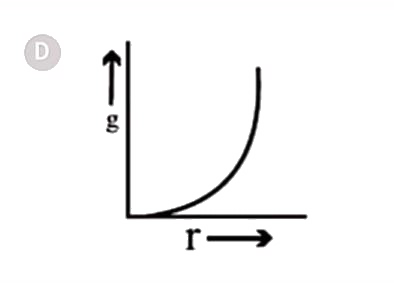
The value of 50 coins of 50 paisa = Rs ________.
View SolutionThe area of a circle (A) varies directly as the square of its radius. The area of the circle of radius 7 cm is 154 cm2. What is the area of the circle of radius 35 cm?
View SolutionThe value of 36 coins of 10paise and 20paise is Rs. 6.60. The number of 10paise coins is
View SolutionFind the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
View SolutionThe radius of a soap bubble is increasing at the rate of 0.2 cm/sec. It its radius is 5 cm, find the rate of increase of its volume.
View Solution