In a municipal parking there are some two wheelers and rest are 4 wheelers. If wheels are counted, there are total 520 wheels but the incharge of the parking told me that there are only 175 vehicles. If no vehicle has a stepney, then the no. of two wheelers is :
75
100
90
85
The correct Answer is:C
To solve the problem step by step, we will define variables and set up equations based on the information provided.
Step 1: Define Variables
Let:
- T = number of two-wheelers
- F = number of four-wheelers
Step 2: Set Up the First Equation
According to the problem, the total number of vehicles is 175. Therefore, we can write the first equation as:
T+F=175
Step 3: Set Up the Second Equation
Next, we know that two-wheelers have 2 wheels each and four-wheelers have 4 wheels each. The total number of wheels counted is 520. Thus, we can write the second equation as:
2T+4F=520
Step 4: Simplify the Second Equation
We can simplify the second equation by dividing all terms by 2:
T+2F=260
Step 5: Set Up the System of Equations
Now we have a system of two equations:
1. T+F=175 (Equation 1)
2. T+2F=260 (Equation 2)
Step 6: Solve the System of Equations
We can subtract Equation 1 from Equation 2 to eliminate T:
(T+2F)−(T+F)=260−175
This simplifies to:
F=85
Step 7: Substitute to Find T
Now that we have F, we can substitute it back into Equation 1 to find T:
T+85=175
Subtracting 85 from both sides gives:
T=175−85
T=90
Conclusion
The number of two-wheelers is T=90.
---
Let:
- T = number of two-wheelers
- F = number of four-wheelers
According to the problem, the total number of vehicles is 175. Therefore, we can write the first equation as:
T+F=175
Next, we know that two-wheelers have 2 wheels each and four-wheelers have 4 wheels each. The total number of wheels counted is 520. Thus, we can write the second equation as:
2T+4F=520
We can simplify the second equation by dividing all terms by 2:
T+2F=260
Now we have a system of two equations:
1. T+F=175 (Equation 1)
2. T+2F=260 (Equation 2)
We can subtract Equation 1 from Equation 2 to eliminate T:
(T+2F)−(T+F)=260−175
This simplifies to:
F=85
Now that we have F, we can substitute it back into Equation 1 to find T:
T+85=175
Subtracting 85 from both sides gives:
T=175−85
T=90
The number of two-wheelers is T=90.
Topper's Solved these Questions
Similar Questions
The number of 2 wheelers are twice the number of 3 wheelers and the number of 4 wheelers are equal to the number of 2 wheelers. Find the average of wheel per vehicle.
View SolutionActivity : Note the frequency of two - wheelers , three - wheelers and four - wheelers going past during a time interval , in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two - wheeler.
View Solution
Knowledge Check
In a munciple parking thereare some two wheelers and rest are 4 wheelers. If wheels are counted, there are total 520 wheels but the incharge of the parking told me that there are only 175 vehicles. If no vehicle has a stepney, then the no. of two wheelers is :
A75B100C90D85There are twice the number of two wheelers as there are three wheelers and the number of 4 wheelers are equal to the number of two wheelers. The average number of wheel per vehicle is :
A3B4C5Dnone of theseThere are twice the number of two wheelers as there are three wheelers and the number of four wheelers are equal to the number of two wheelers. The average of wheel per vehicle is :
A3B4C5Dnone of these
In an autofair at Pragati Maidan, New Delhi, there are 600 vehicles consisting of only two wheelers and four whellers. A world renowned tyre agency visits the fair to survey the trye market which finds that there are total 2000 tyres are fixed in all the 600 vehicles, but without any stepney (or spare tyre). The number of two wheelers in the autofair is :
View SolutionIn an autofair at Pragati Maidan, New Delhi, there are 600 vehicles consisting of only two wheelers and four whellers. A world renowned tyre agency visits the fair to survey the trye market which finds that there are total 2000 tyres are fixed in all the 600 vehicles, but without any stepney (or spare tyre). The number of two wheelers in the autofair is :
View SolutionThere are some four-wheelers and six-wheelers in a garage. The total number of wheels of these vehicles is 120. The number of four-wheelers is 3/2 times the number of six-wheelers. Find the number of six-wheelers in the garage.
View Solution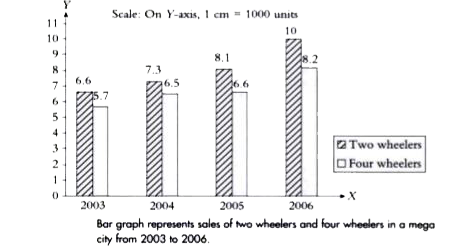
Total number of vehicles (two wheelers and four wheelers) sold in the years 2003 and 2004 is________
View SolutionThere are some four-wheelers and six-wheelers in a garage. The total number of wheels of these vehicles is 120. The number of four-wheelers is 3/2 times the number of six-wheelers. Find the number of six-wheelers in the garage.
View Solution
