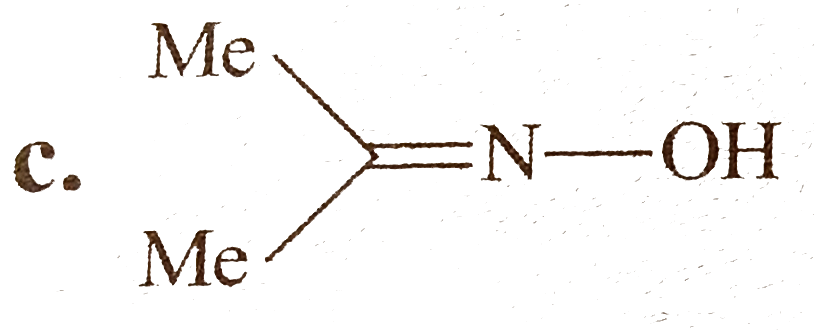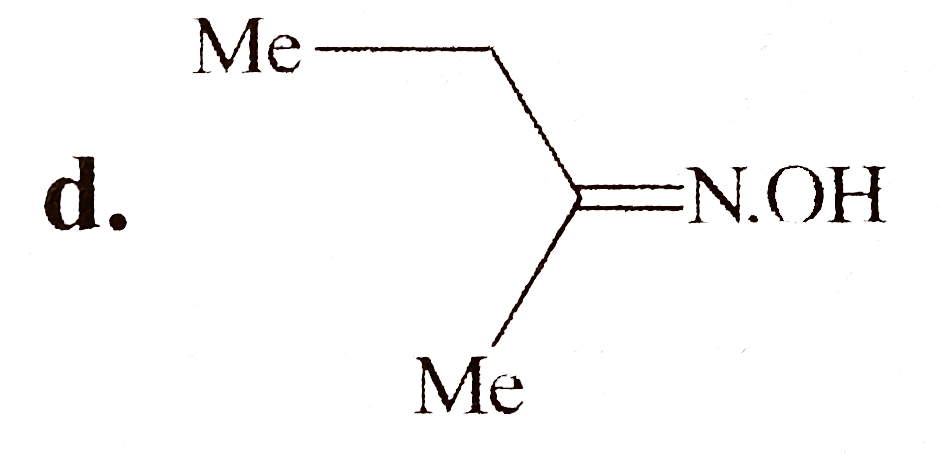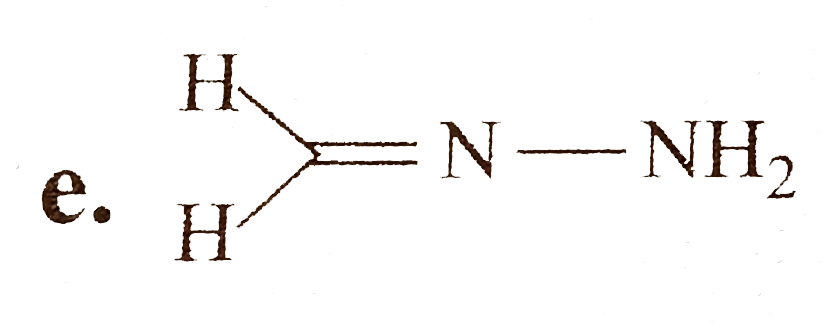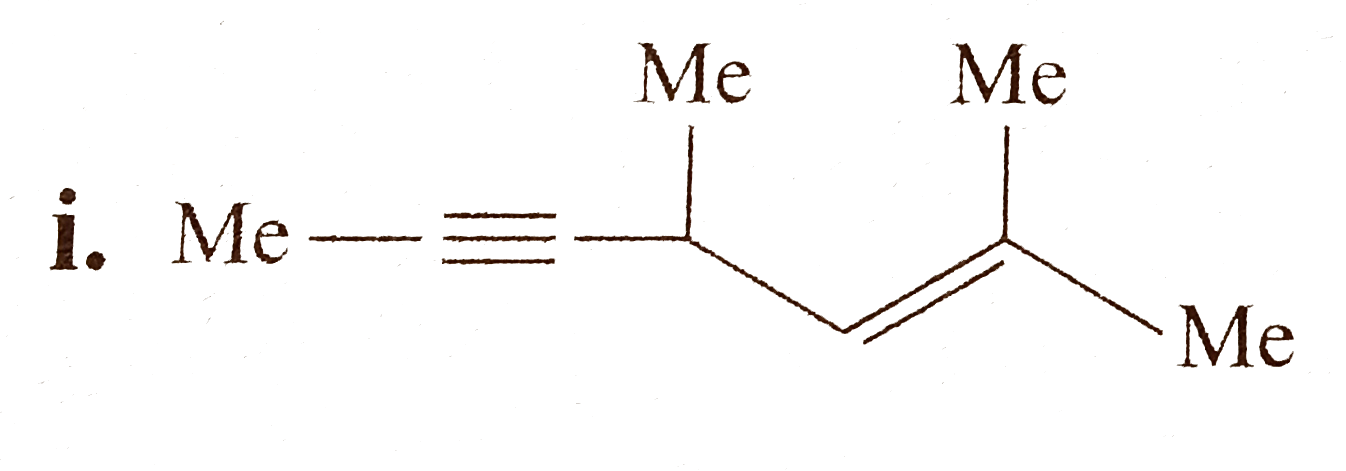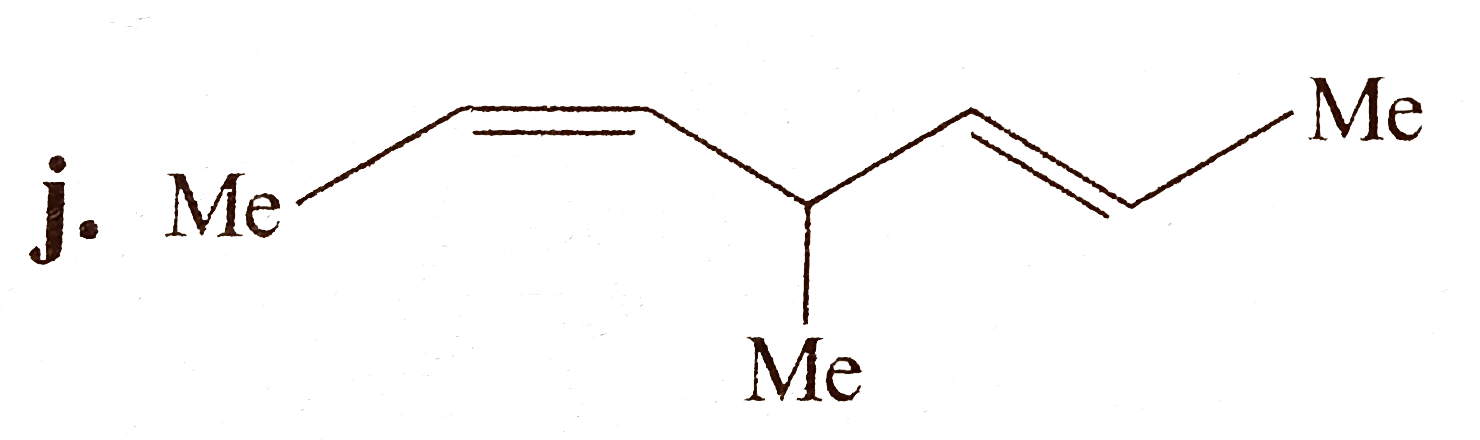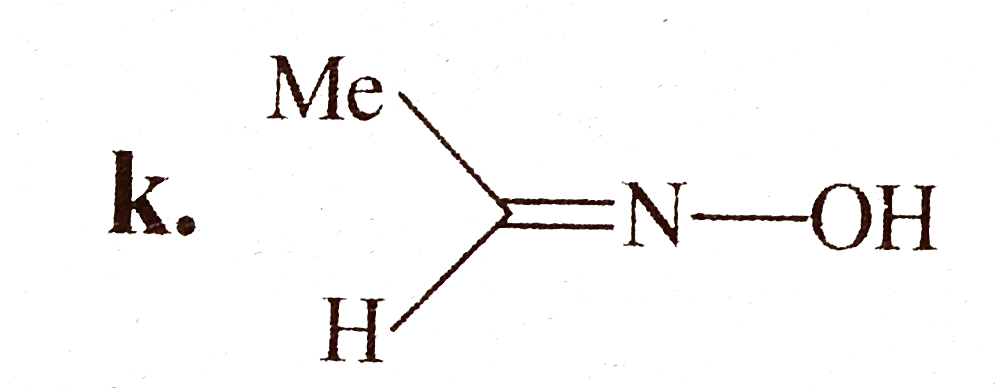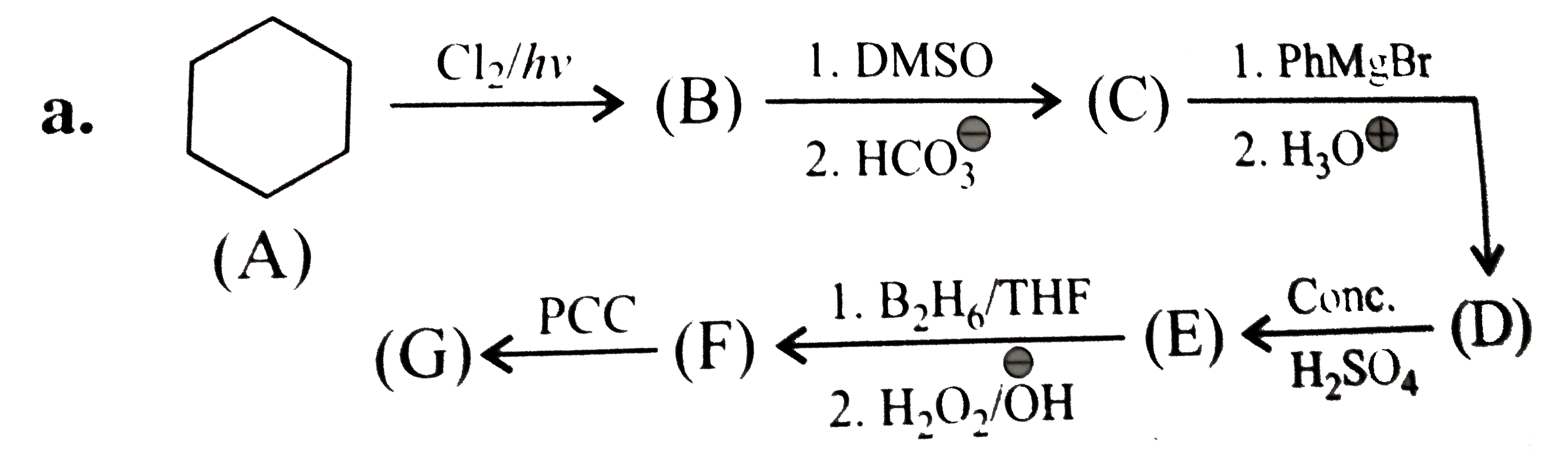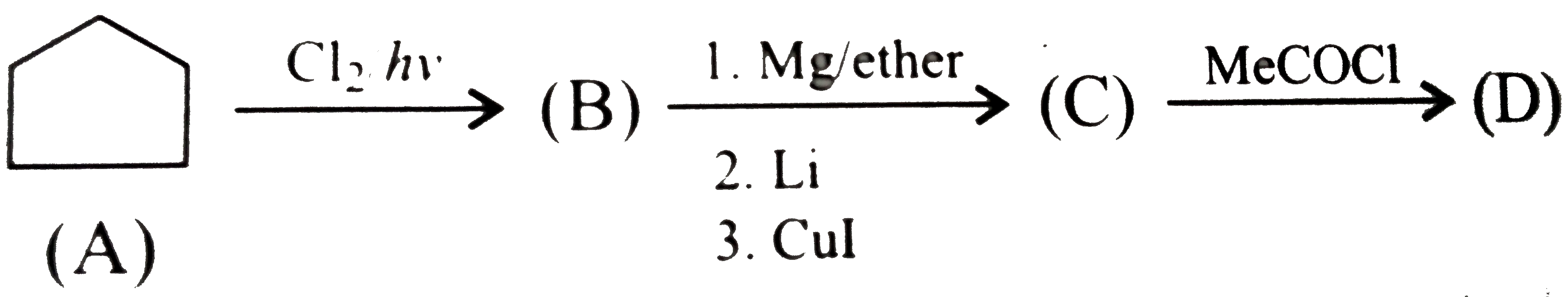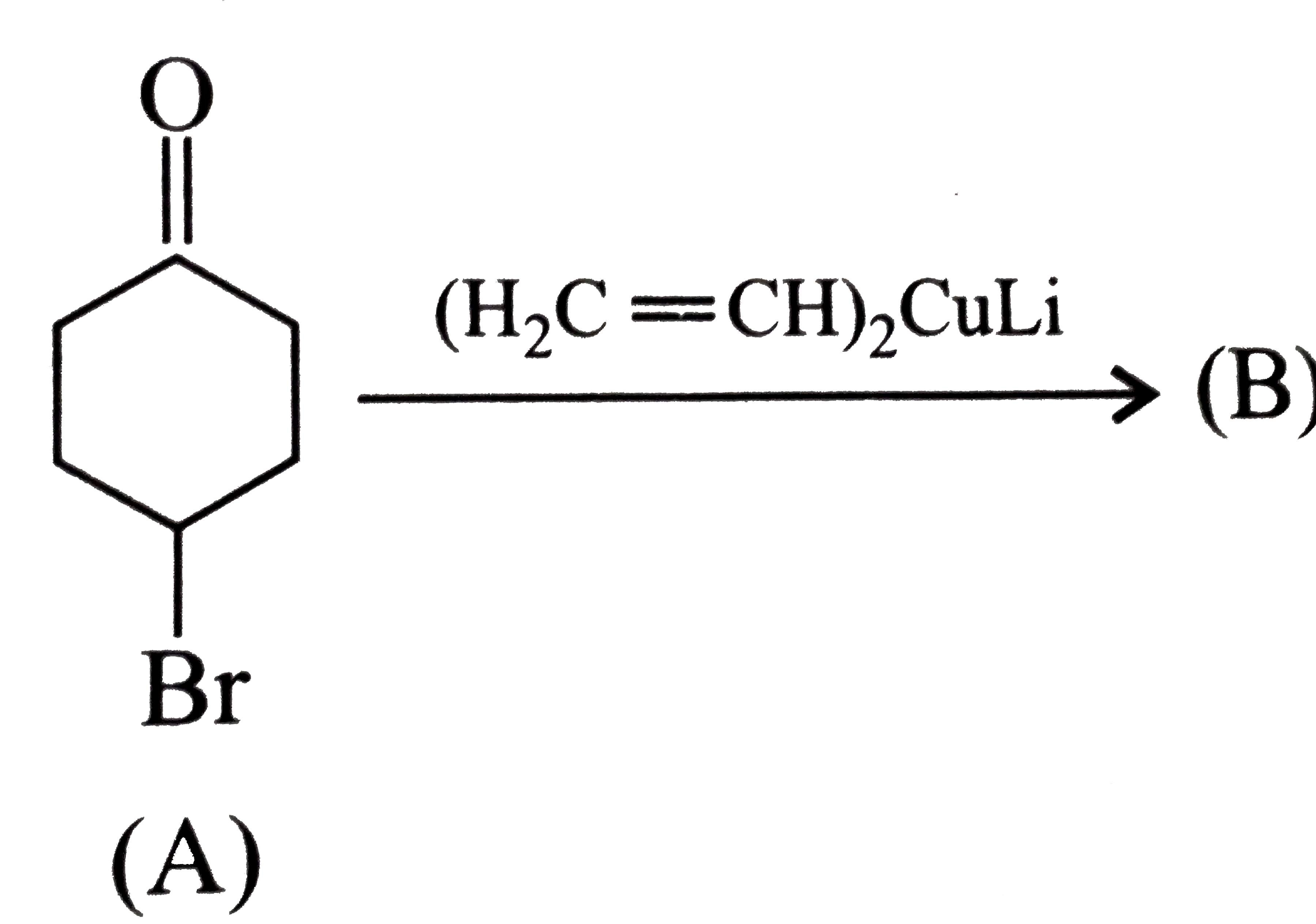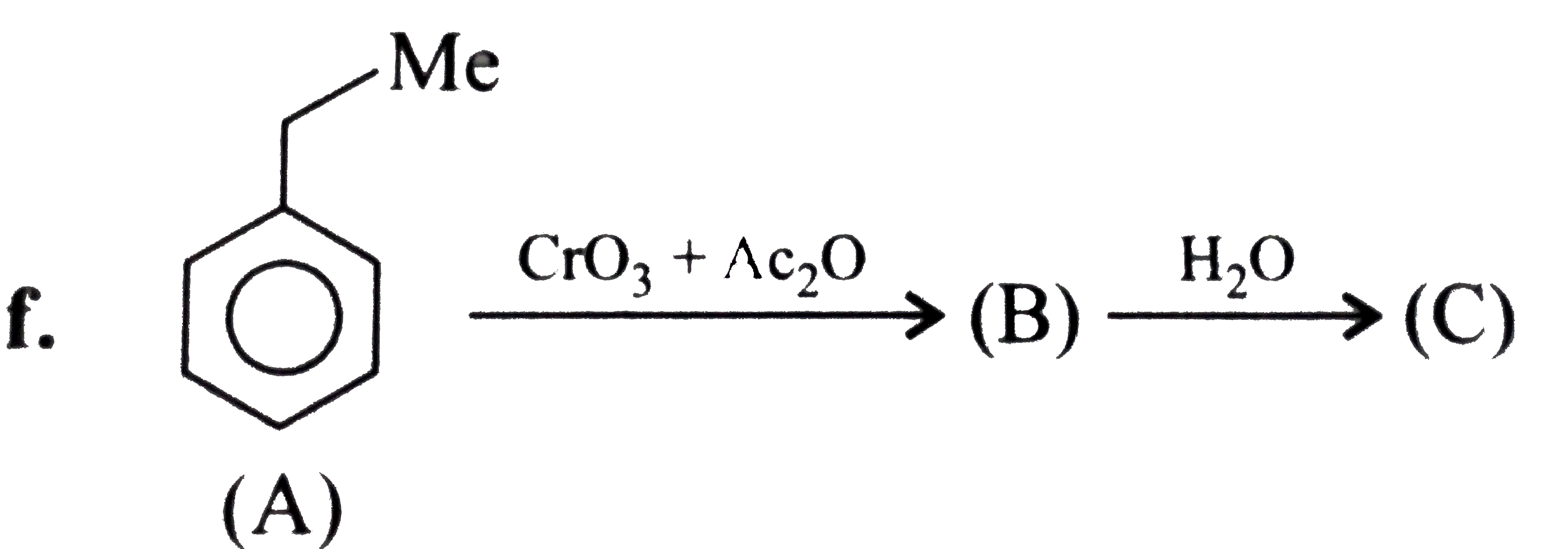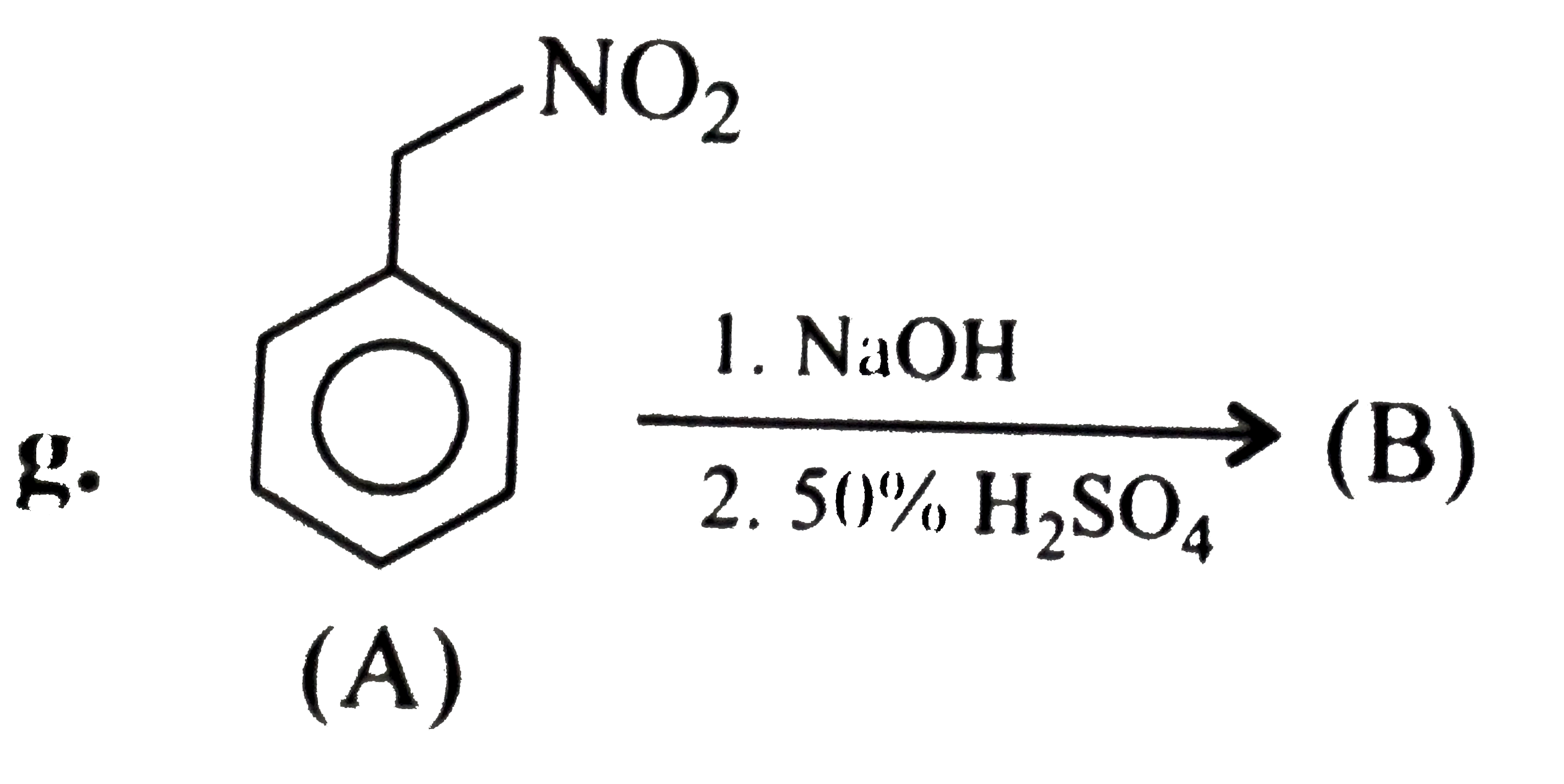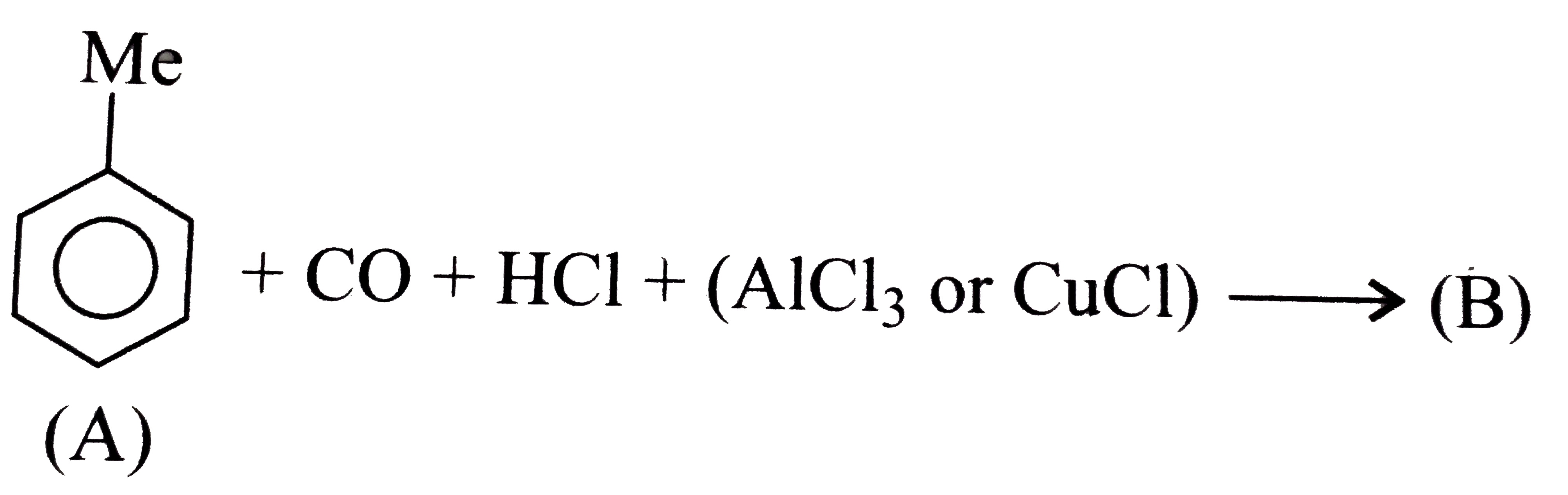If F=a.(|b|).c.(|d|).e.(|f|).g(|h|).i.(|j|) and G=a.b.c.d.e.f.g.h.i.j Again, a=(−1)1,b=(2)−2,c=(−3)3,d=(4)−4,…..j=(10)−10 then the correct relation is :
F=−G
F=G
F.G=1
None of these
The correct Answer is:B
To solve the problem, we need to evaluate the expressions for F and G given the values of a through j.
Step 1: Define the values of a through j
Given:
- a=(−1)1=−1
- b=2−2=122=14
- c=(−3)3=−27
- d=4−4=144=1256
- e=(−5)5=−3125
- f=6−6=166=146656
- g=7−7=177
- h=(−8)8=88 (which is positive)
- i=9−9=199
- j=10−10=11010
Step 2: Calculate F
The expression for F is:
F=a⋅|b|⋅c⋅|d|⋅e⋅|f|⋅g⋅|h|⋅i⋅|j|
Substituting the values:
F=(−1)⋅∣∣∣14∣∣∣⋅(−27)⋅∣∣∣1256∣∣∣⋅(−3125)⋅∣∣∣146656∣∣∣⋅(177)⋅88⋅(199)⋅(11010)
Step 3: Simplify F
Calculating the absolute values:
F=(−1)⋅14⋅(−27)⋅1256⋅(−3125)⋅146656⋅177⋅88⋅199⋅11010
Now, count the negative signs:
- There are 3 negative terms: (−1),(−27),(−3125), which results in a negative product.
Thus, we can rewrite F as:
F=−(14⋅27⋅1256⋅3125⋅146656⋅177⋅88⋅199⋅11010)
Step 4: Calculate G
The expression for G is:
G=a⋅b⋅c⋅d⋅e⋅f⋅g⋅h⋅i⋅j
Substituting the values:
G=(−1)⋅14⋅(−27)⋅1256⋅(−3125)⋅146656⋅177⋅88⋅199⋅11010
Step 5: Simplify G
Counting the negative signs:
- There are 3 negative terms: (−1),(−27),(−3125), which results in a negative product.
Thus, we can rewrite G as:
G=−(14⋅27⋅1256⋅3125⋅146656⋅177⋅88⋅199⋅11010)
Step 6: Compare F and G
From the simplifications, we see that:
F=−G
Conclusion
The correct relation is:
F=−G
- a=(−1)1=−1
- b=2−2=122=14
- c=(−3)3=−27
- d=4−4=144=1256
- e=(−5)5=−3125
- f=6−6=166=146656
- g=7−7=177
- h=(−8)8=88 (which is positive)
- i=9−9=199
- j=10−10=11010
F=a⋅|b|⋅c⋅|d|⋅e⋅|f|⋅g⋅|h|⋅i⋅|j|
F=(−1)⋅∣∣∣14∣∣∣⋅(−27)⋅∣∣∣1256∣∣∣⋅(−3125)⋅∣∣∣146656∣∣∣⋅(177)⋅88⋅(199)⋅(11010)
F=(−1)⋅14⋅(−27)⋅1256⋅(−3125)⋅146656⋅177⋅88⋅199⋅11010
- There are 3 negative terms: (−1),(−27),(−3125), which results in a negative product.
F=−(14⋅27⋅1256⋅3125⋅146656⋅177⋅88⋅199⋅11010)
G=a⋅b⋅c⋅d⋅e⋅f⋅g⋅h⋅i⋅j
G=(−1)⋅14⋅(−27)⋅1256⋅(−3125)⋅146656⋅177⋅88⋅199⋅11010
- There are 3 negative terms: (−1),(−27),(−3125), which results in a negative product.
G=−(14⋅27⋅1256⋅3125⋅146656⋅177⋅88⋅199⋅11010)
F=−G
F=−G
Topper's Solved these Questions
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.1
34 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.2
16 Videos
- FUNCTIONS AND GRAPHBOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round
40 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
Similar Questions
Knowledge Check
If F=a.(|b|).c.(|d|).e.(|f|).g(|h|).i.(|j|) and G=a.b.c.d.e.f.g.h.i.j Again, a=(−1)1,b=(2)−2,c=(−3)3,d=(4)−4,…..j=(10)−10 then the correct relation is :
AF = -GBF = GCF.G = 1Dnone of theseIf ab=cd=ef=34, what is the value of a+c+eb+d+f?
Aa) 9/16Bb) 3/4Cc) 2/3Dd) 4/5
Calculate the Land'e g factor for atoms
(a).6F1/2, (b) .4D1/2, (c ).5F2, (d) .5P1, (e ) .3P0
View SolutionLet R be a relation such that R={(a d) (c g) (d e) (d f) (g f)} then (ROR^(1))^(-1) is
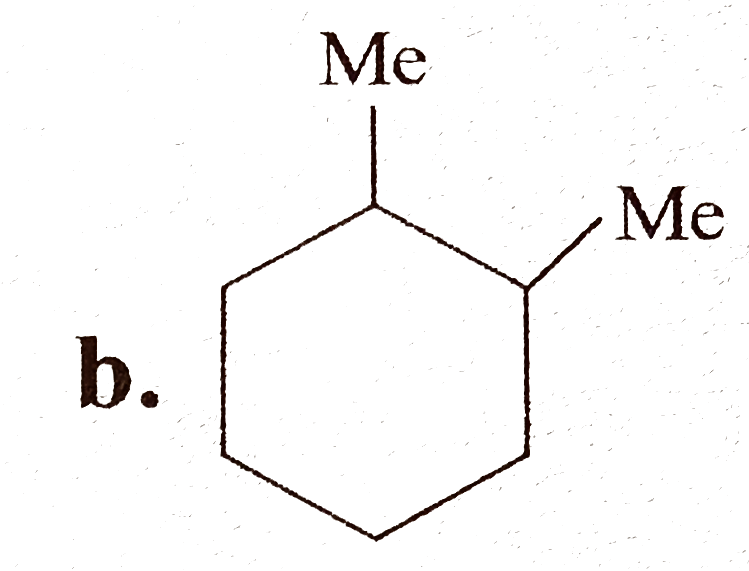
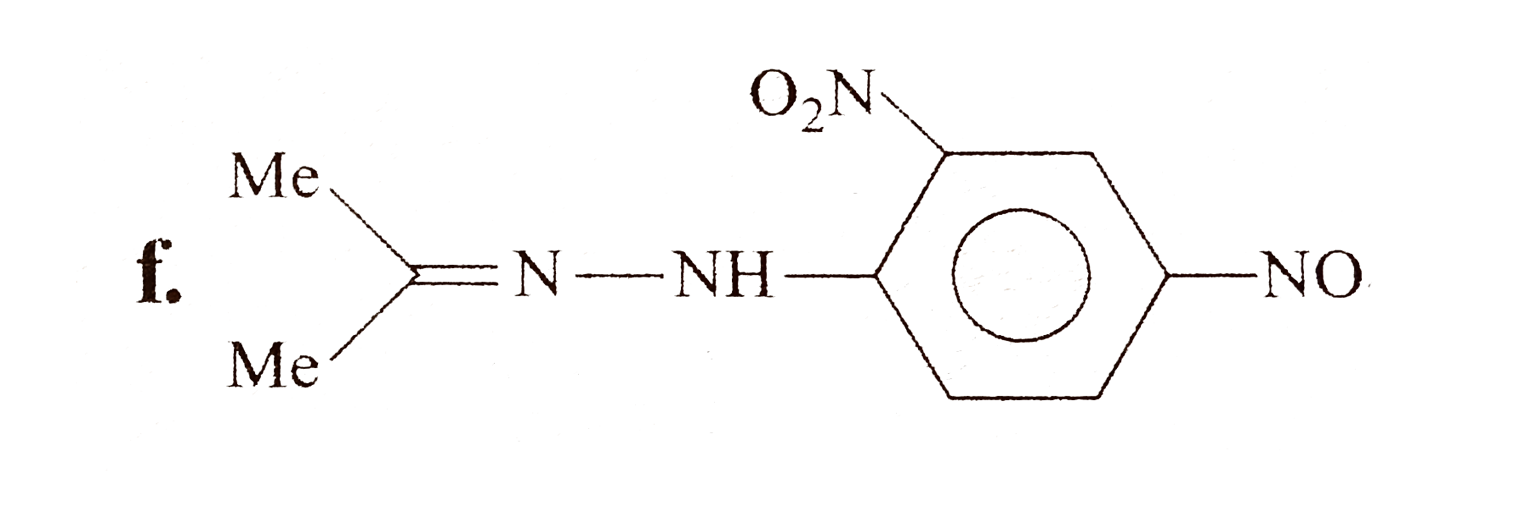
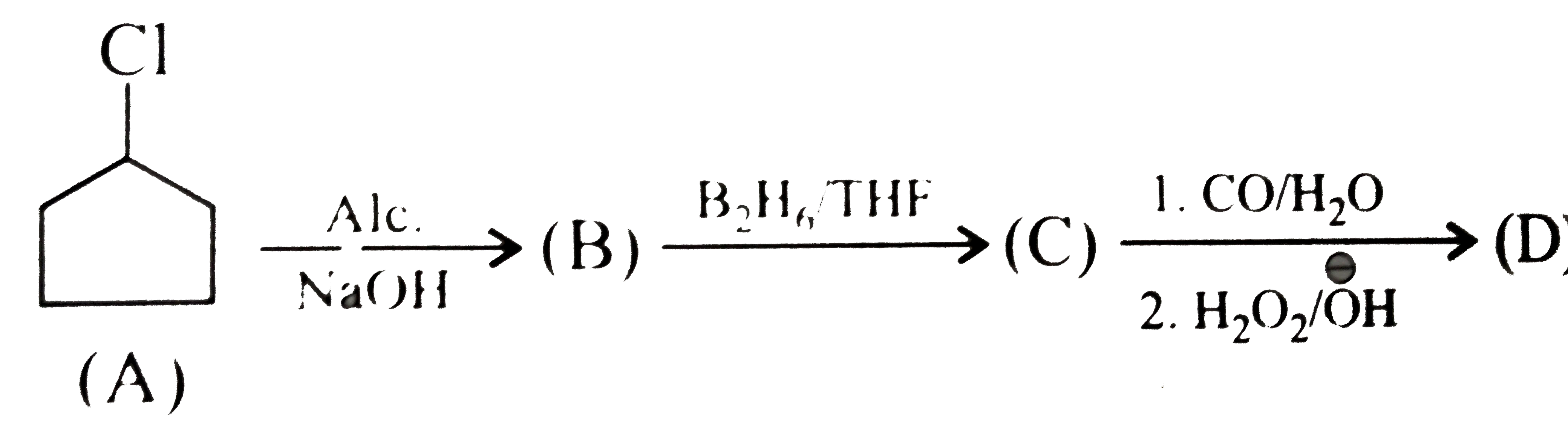
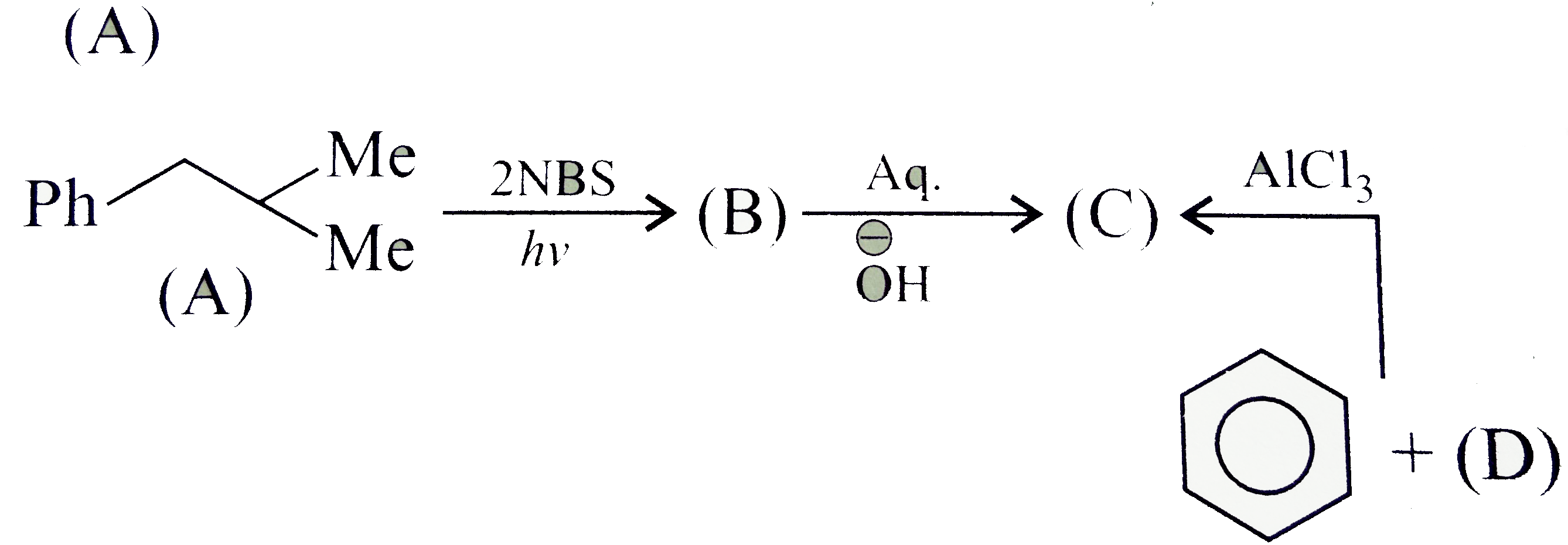
View SolutionIdentify the products and explain their formation.
(a)
(b)
( c)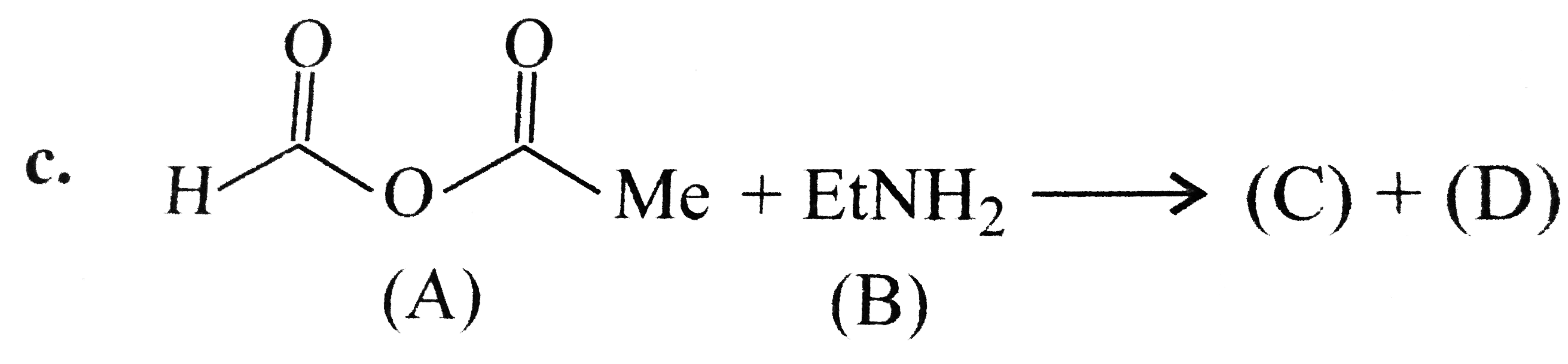
(d)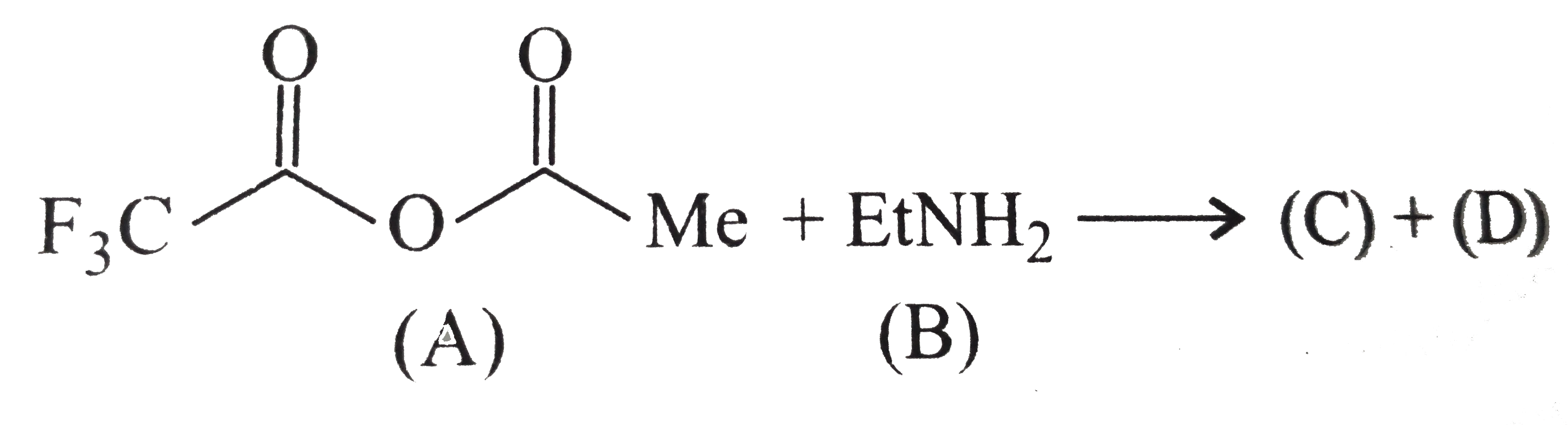
( e)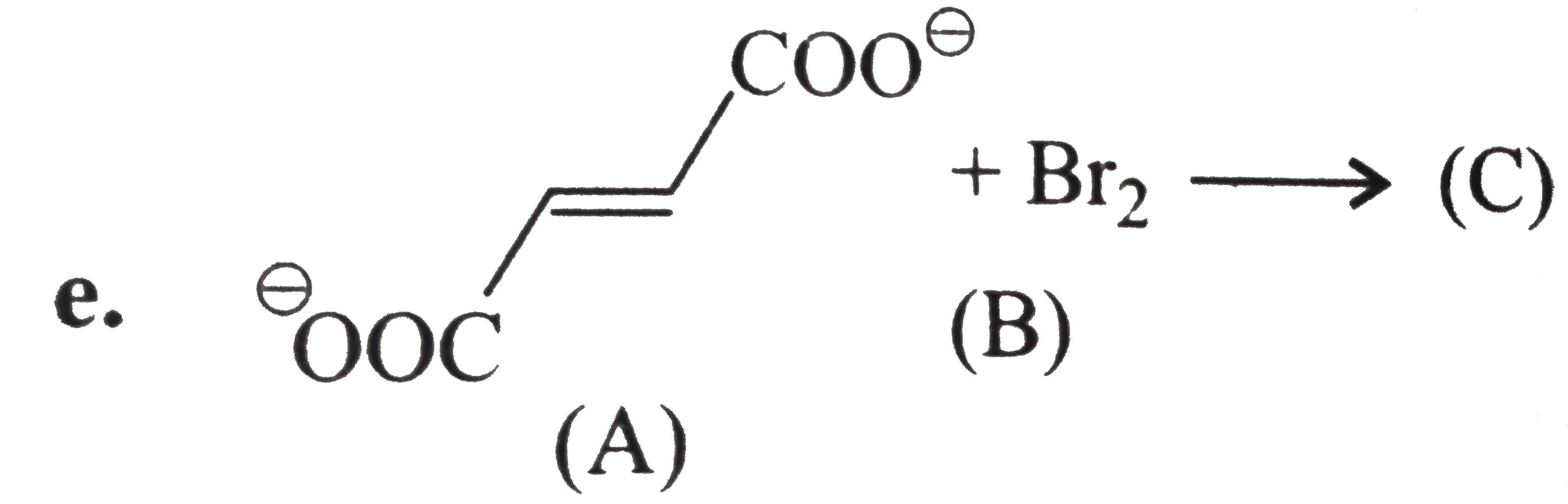
(f)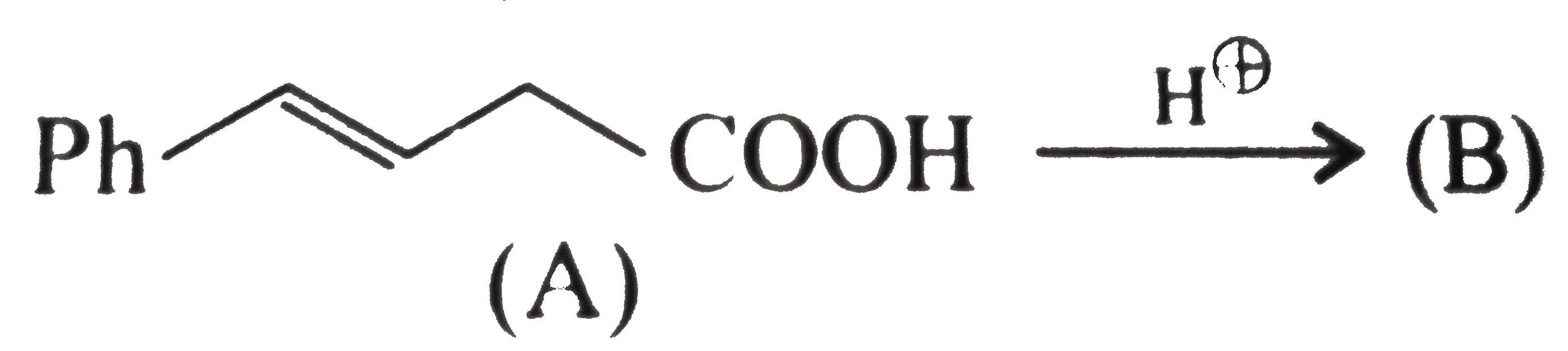
(g)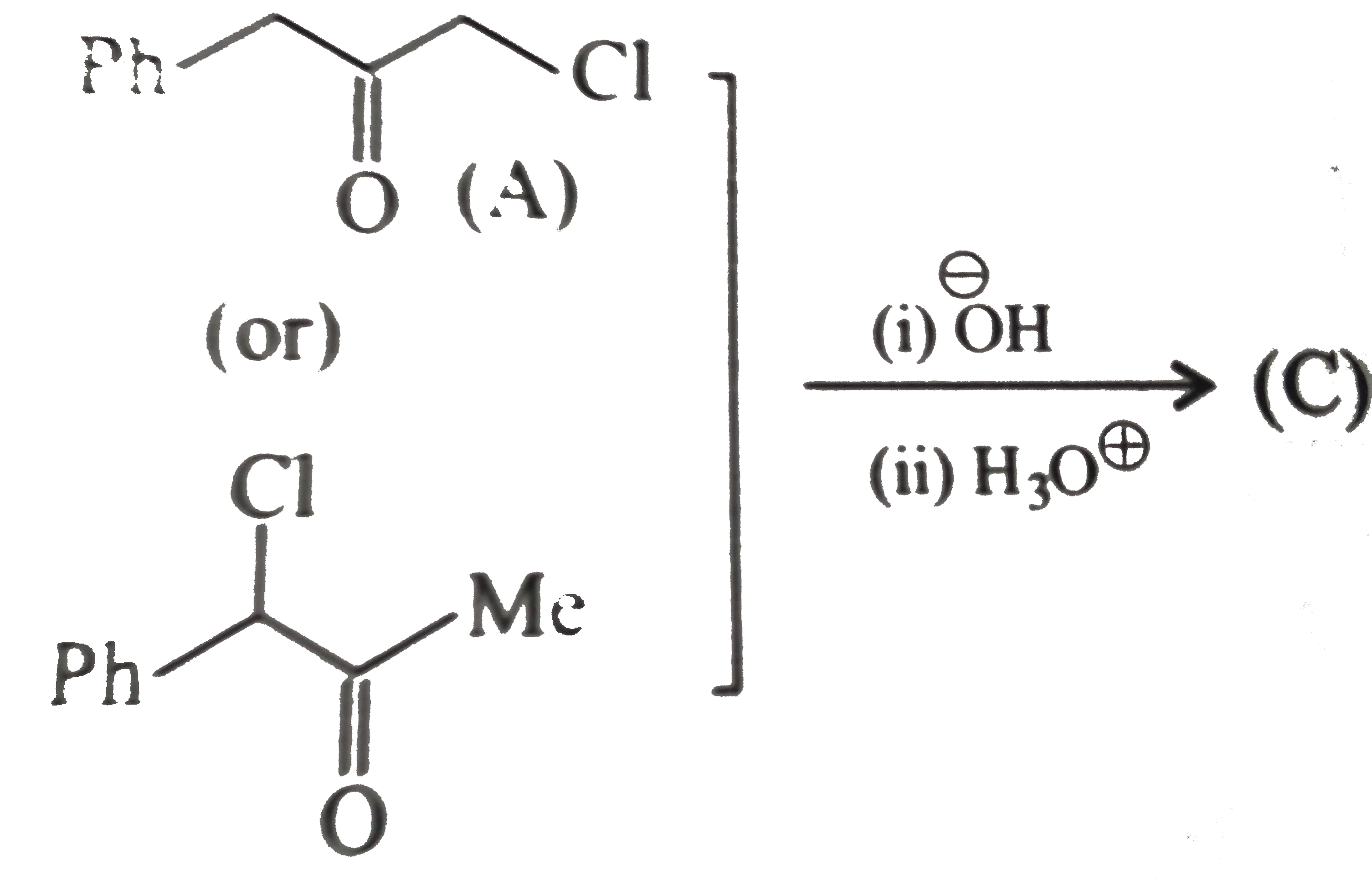
(h)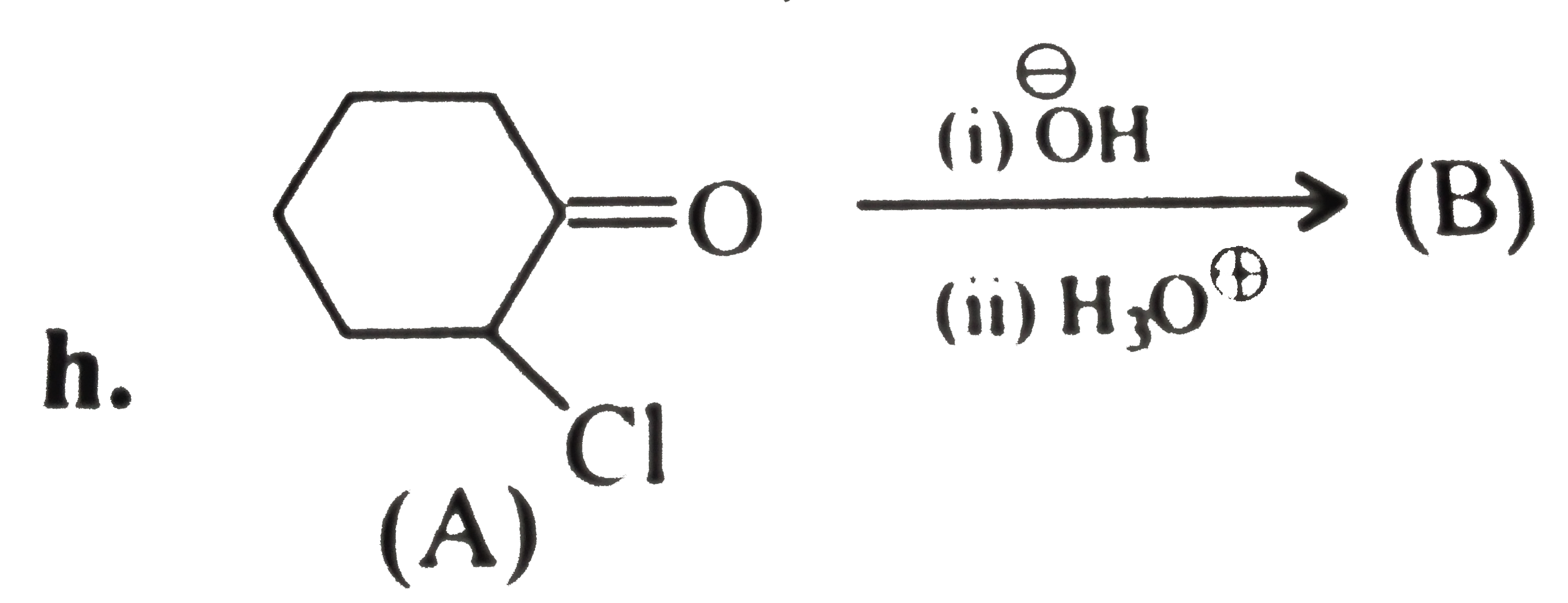
(i)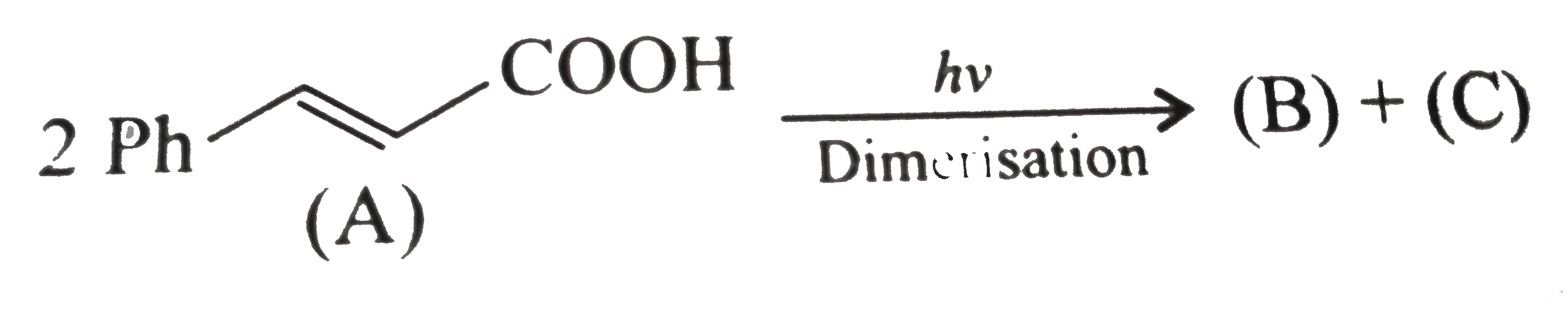 .
.
View SolutionIf A={a,b,c,d,e},B={a,c,e,g}andC={b,e,f,g}verify that :
(i)A∩(B−C)=(A∩B)−(A∩C)
(ii) A−(B∩C)=(A−B)∪(A−C)
View SolutionIn Fig.97, If AB is parallel to CD, then the value of ∠BPE is (a) (b)(c)(d)(e)106(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)76(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)74(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)84(q)0(r)(s)(t) (u)
View SolutionTwo complementary angles are in the ratio 2:3. The measure of the larger angle is (a) (b)(c)(d)(e)60(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)54(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)66(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)48(q)0(r)(s)(t) (u)
View Solution