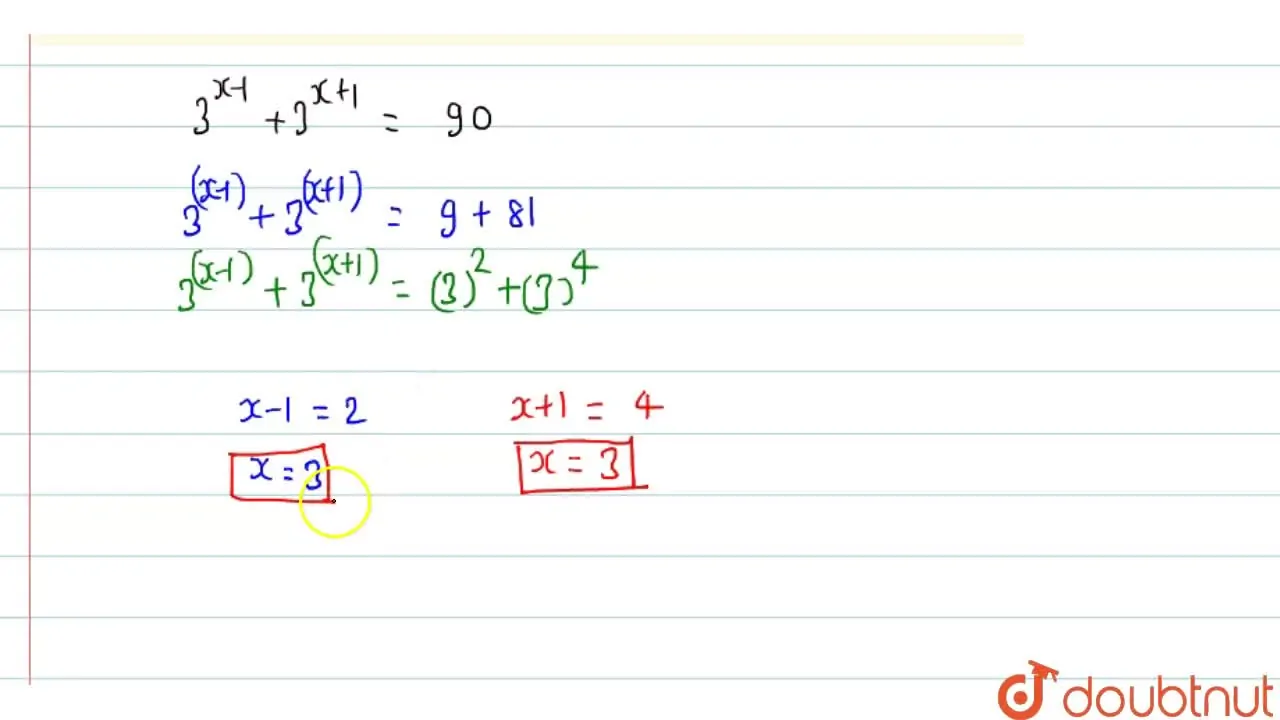Solve the following expressions .
3x−1+3x+1=90 then x = ?
The correct Answer is:3
Step by step video, text & image solution for Solve the following expressions . 3^(x - 1) + 3^(x + 1) = 90 then x = ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.134videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.216videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round40videos
FUNCTIONS AND GRAPH
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
Similar Questions
Solve the following expressions .
42x+1=8x+3, then x = ?View SolutionSolve the following expressions .
22x−1=18x−3, then x = ?View SolutionSolve the following expressions.
22x+1=8x+3 then x = ?View SolutionSolve the following expressions.
22x−2=116x−3 then x = ?View SolutionSolve the following 1≤|x−2|≤3
View SolutionSolve the following equation :
7(x+1)=5(x−3)View SolutionSolve the following linear inequation in R:3x−7>x+1
View SolutionSolve each of the following equatins :
x=3x+14xView SolutionSolve the following linear inequation in R:x−1x+3>2
View SolutionSolve the following equation: |x−2|x−3=1x−3
View Solution