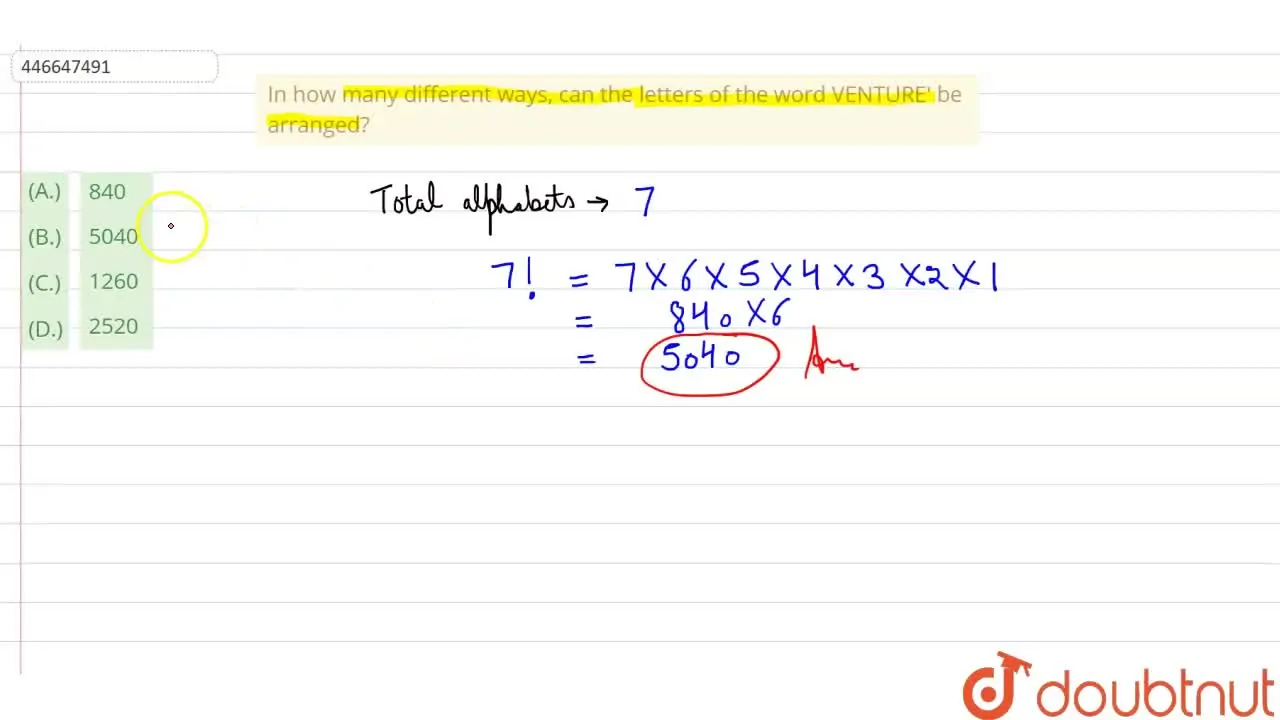
In how many different ways, can the letters of the word VENTURE' be arranged?
840
5040
1260
2520
The correct Answer is:D
Step by step video, text & image solution for In how many different ways, can the letters of the word VENTURE' be arranged? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
- BOOK - ARIHANT SSCCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - HIGHER SKILL LEVEL QUESTIONS19videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT SSCCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - HIGHER SKILL LEVEL QUESTIONS19videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT SSCCHAPTER - PERMUTATIONS & COMBINATIONS EXERCISE - FINAL ROUND38videos
PERMUTATIONS & COMBINATIONS
- BOOK - ARIHANT SSCCHAPTER - PIE CHART EXERCISE - Exercise Higher Skill Level Questions15videos
PIE CHART
Similar Questions
In how many different ways can the letters of the word ‘PRESENT’ be arranged?
View SolutionIn how many different ways, can the letters of the word 'INHALE' be arranged?
View SolutionIn how many different ways can the letters of the word 'PRUDENT' be arranged?
View SolutionIn how many different ways can the letters of the word 'SERIES' be arranged?
View SolutionIn how many different ways can the letters of the word 'NUMBER' be arranged?
View SolutionIn how many different ways can the letters of the word 'DESIRE' be arranged?
View SolutionIn how many different ways can the letters of the word 'TROUBLE' be arranged ?
View SolutionIn how many different ways can the letters of the word 'PRIDE' be arranged?
View SolutionIn how many different ways can the letters of the word 'SEQUENCE' be arranged ?
View SolutionIn how many different ways can the letters of the word 'CREAM' be arranged ?
View Solution