There are three stations A, B and C and five routes for going from station A to B and four routes from station B to C. Find the number of different ways through which a person can go from A to C via B.
The correct Answer is:20
To solve the problem of finding the number of different ways a person can go from station A to station C via station B, we can break down the solution into clear steps.
1. Identify the Routes from A to B:
- There are 5 different routes available for traveling from station A to station B.
2. Identify the Routes from B to C:
- There are 4 different routes available for traveling from station B to station C.
3. Calculate the Total Ways from A to C via B:
- To find the total number of different ways to travel from A to C via B, we multiply the number of routes from A to B by the number of routes from B to C.
- This can be expressed mathematically as:
Total Ways=(Ways from A to B)×(Ways from B to C)=5×4
4. Perform the Multiplication:
- Calculate 5×4:
5×4=20
5. Conclusion:
- Therefore, the total number of different ways a person can go from station A to station C via station B is 20.
Final Answer:
The number of different ways through which a person can go from A to C via B is 20.
---
- There are 5 different routes available for traveling from station A to station B.
- There are 4 different routes available for traveling from station B to station C.
- To find the total number of different ways to travel from A to C via B, we multiply the number of routes from A to B by the number of routes from B to C.
- This can be expressed mathematically as:
Total Ways=(Ways from A to B)×(Ways from B to C)=5×4
- Calculate 5×4:
5×4=20
- Therefore, the total number of different ways a person can go from station A to station C via station B is 20.
The number of different ways through which a person can go from A to C via B is 20.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBook:ARIHANT SSCChapter:PERMUTATIONS AND COMBINATIONSExercise:EXERCISE BASE LEVEL QUESTIONS
Explore 30 Videos
- PERMUTATIONS AND COMBINATIONSBook:ARIHANT SSCChapter:PERMUTATIONS AND COMBINATIONSExercise:HIGHER SKILL LEVEL QUESTIONS
Explore 19 Videos
- PERMUTATIONS & COMBINATIONS Book:ARIHANT SSCChapter:PERMUTATIONS & COMBINATIONS Exercise:FINAL ROUND
Explore 38 Videos
- PIE CHART Book:ARIHANT SSCChapter:PIE CHART Exercise:Exercise Higher Skill Level Questions
Explore 15 Videos
Similar Questions
There are three stations A,B and C five routes for going from station A to station B and four routes for going from station B to station C. find number of different ways through which a person can go from A to C via B.
View SolutionThere are 5 routes ferom A to B and 3 routes from place B to place C. Find how many different routes are there from A to C via B.
View Solution
Knowledge Check
There are five routes for going from station A to station B and four routes for going from station B to station C. Find the number of different ways in which a person can go from A to C via B.
A9B20C16Dnone of these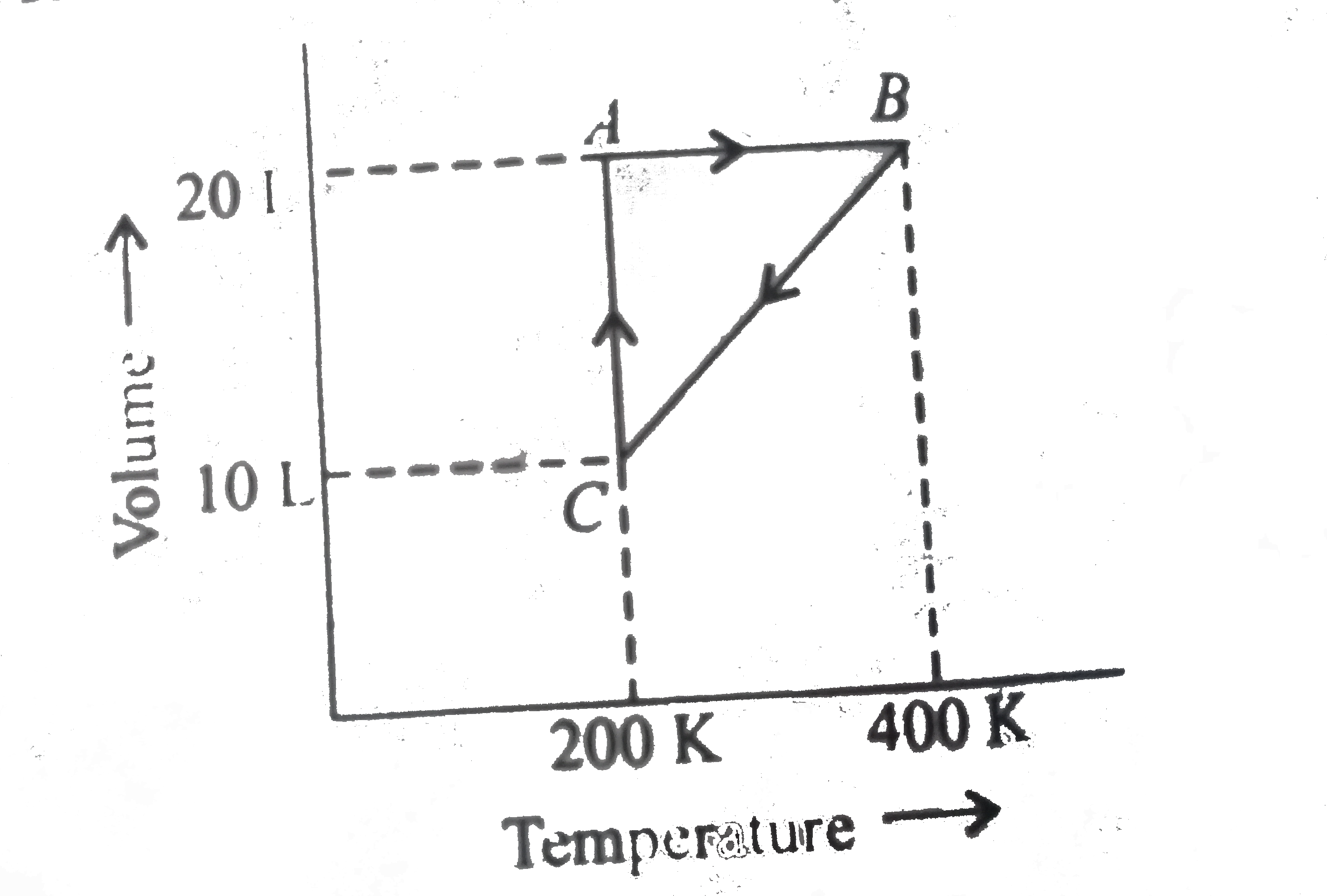
The process which occurs in going from B→C isAIsothermalBAdiabaticCIsobaricDIsochoric
A person wants to leave station B. There are three routes from station B to A and four routes from B to c. In how many ways can he leave the station B.
View SolutionThere are 4 routes for going from Dumdum to Sealdah and 5 routes for going from Sealdah to Chandni. In how many different ways can you go from Dumdum to via Sealdah?
View SolutionThere are 3 routes from Guntur to Madras and 4 routes from Madras to Cochin,in how many different ways a person can travel from Guntur to Cochin via Madras is
View SolutionA, B and C are three cities. There are 5 routes from A to B and 3 routes from B to C. How many different routes are there from A to C via B?
View SolutionThere are 10 railway stations between a station X and another station Y. Find the number of different tickets that must be printed so as to enable a passenger to travel from one station to any other.
View SolutionA person wants to leave station Q. There are 4 routes from station Q to P and 5 routes from Q to R. In how many ways can he travel from the station Q ?
View Solution
