The number of solutions of the equation
e|sinx|=secx for all x∈(−π/2,π/2) is/are
A
1
B
3
C
5
D
2
Video Solution
Text Solution
The correct Answer is:B
Clearly, curves y=e|sinx| and y=sec x intersect at three points for all x∈(−π/2,π/2).
Hence, the given equation has three solutions in (−π/2,π/2).
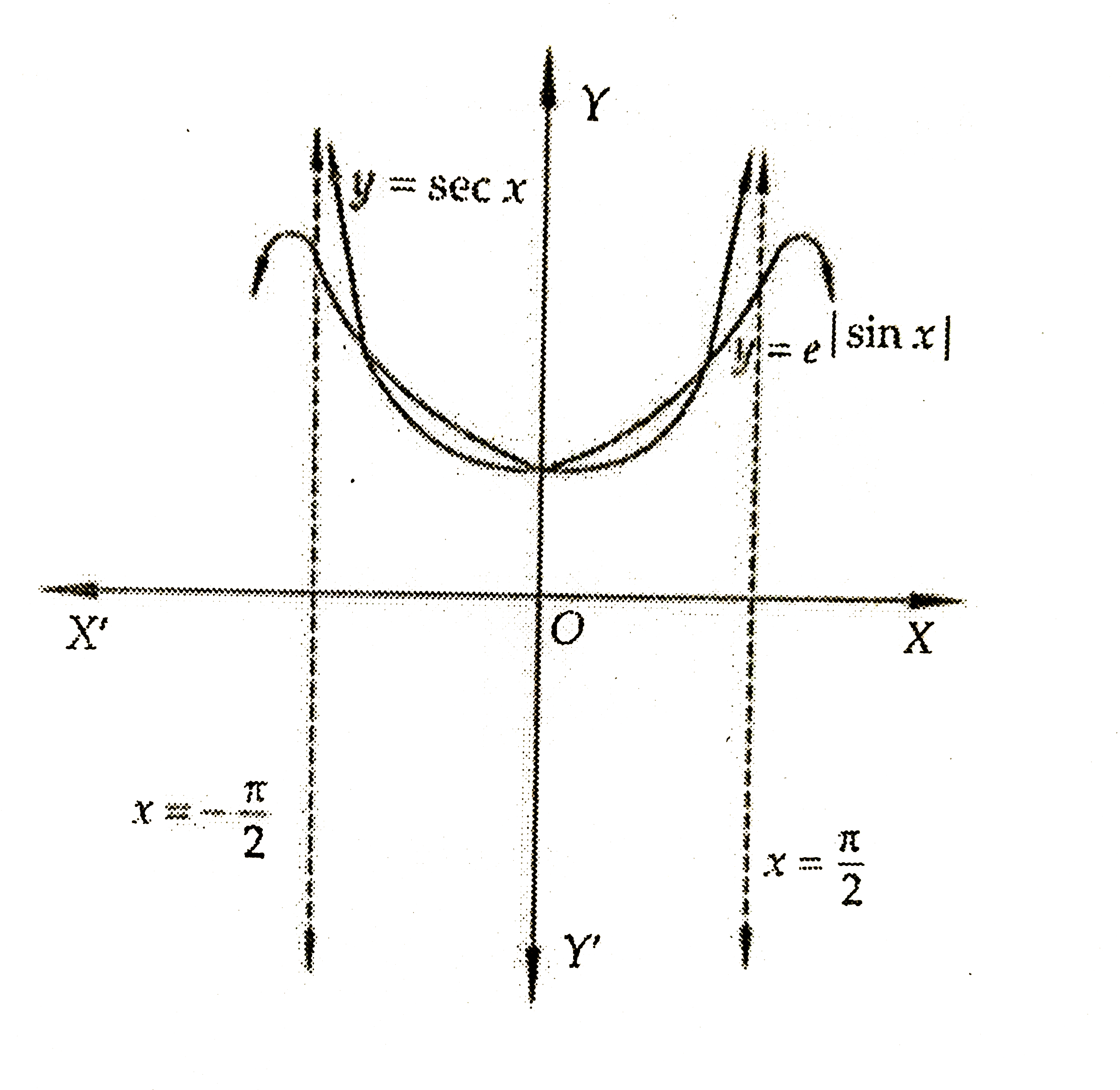
|
Topper's Solved these Questions
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Exercise
30 Videos
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Chapter Test
30 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMACHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMACHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
Similar Questions
Knowledge Check
The number of solutions of the equation tanx+secx=2cosx,x∈[0,2π] is
A1B2C3D0The number of solutions of equations |tan2x|=sinx in[0,π]
A2B4C6D8Find the number of solution of the equation 30|sinx|=xin0≤x≤2π
A4B2C8D6
The number of solutions of the equation lsinx|=|cos3xl in [−2π,2π]
View SolutionThe number of solution (s) of the equation
√2+cos2x=(sinx+cosx)∈[−π2,π]
View SolutionThe number of solutions of the equation 2cosx=|sinx| in [−2π,2π] is
View SolutionThe number of solution of the equation |sinx|=|cos3x| in [−2π,2π] is
View SolutionThe number of solutions of the equation 1+sin4x=cos23x,x∈[−5π/2,5π/2] is
View Solution
