यदि (x−1)3(x+1)<0 तब x∈
A
(−1,1)
B
(−∞,−1)
C
[−1,1]
D
(−1,∞)
Video Solution
Text Solution
The correct Answer is:A
We have,
(x−1)3(x+1)<0
⇒(x−1)2(x−1)(x+1)>0
⇒(x−1)(x+1)<0 [∵(x−1)2≥0for all x∈R]
⇒−1<x<1⇒x∈(−1,1)
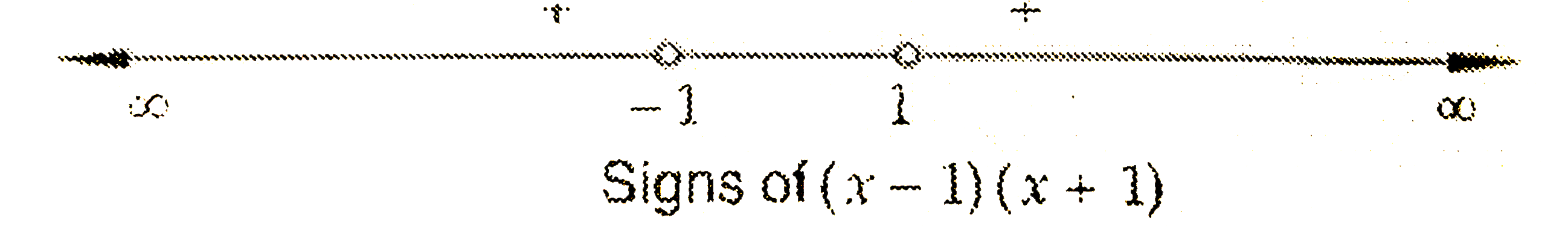
|
Topper's Solved these Questions
- ALGEBRAIC INEQUATIONSBook:OBJECTIVE RD SHARMAChapter:ALGEBRAIC INEQUATIONSExercise:Section I - Solved Mcqs
Explore 20 Videos
- ALGEBRAIC INEQUATIONSBook:OBJECTIVE RD SHARMAChapter:ALGEBRAIC INEQUATIONSExercise:Exercise
Explore 39 Videos
- ALGEBRA OF VECTORSBook:OBJECTIVE RD SHARMAChapter:ALGEBRA OF VECTORSExercise:Chapter Test
Explore 30 Videos
- APPLICATION OF DERIVATIVESBook:OBJECTIVE RD SHARMAChapter:APPLICATION OF DERIVATIVESExercise:Illustration
Explore 6 Videos
Similar Questions
Knowledge Check
यदि x−12≥2, तब x∈
A(1, 2)B(0, 1)C[5,∞)D(1,∞)What is the minimum value of [x(x−1)+1]13 where 0<x<1 ?
A(34)13B1C13D(38)13The function f(x)=⎧⎪⎨⎪⎩5x−4 for 0<x≤14x2−3x for1<x<23x+4forx≥2is
Acontinuous at x-1 and x=2Bcontinuous at x=1 but not derivable at x=2Ccontinuous at x=1 and 2 but not derivable at x=1Dcontinuous at x=1 and 2 but not derivable derivable at x=1 and x=2
Solve : (|x−1|−3)(∣x+2)−5)<0.
View SolutionIf (sin−1x)2−(cos−1x)2=a , 0<x<1, a≠0, then the value of 2x2−1 is
View SolutionProve the inequalities
1+12x−x28<√1+x<1+12x at 0<x<∞
View SolutionIf log0.3(x−1)<log0.09(x−1), then x lies in the interval
View SolutionThe sum of the infinite series 1+(1+a)x+(1+a+a2)x2+(1+a+a2+a3)x3+… where 0<a,x<1, is
View Solution

