let A(x1,0) and B(x2,0) be the foci of the hyperbola x29−y216=1 suppose parabola having vertex at origin and focus at B intersect the hyperbola at P in first quadrant and at point Q in fourth quadrant.
(−910,0)
(23,0)
(910,0)
(23,√6)
The correct Answer is:A
Here , x29+y28=1
has foci (+ae,0)
where , a2e2=a2−b2
⇒a2e2=9−8
⇒ae=±1
i.e.,F1,F2=(±1,0)
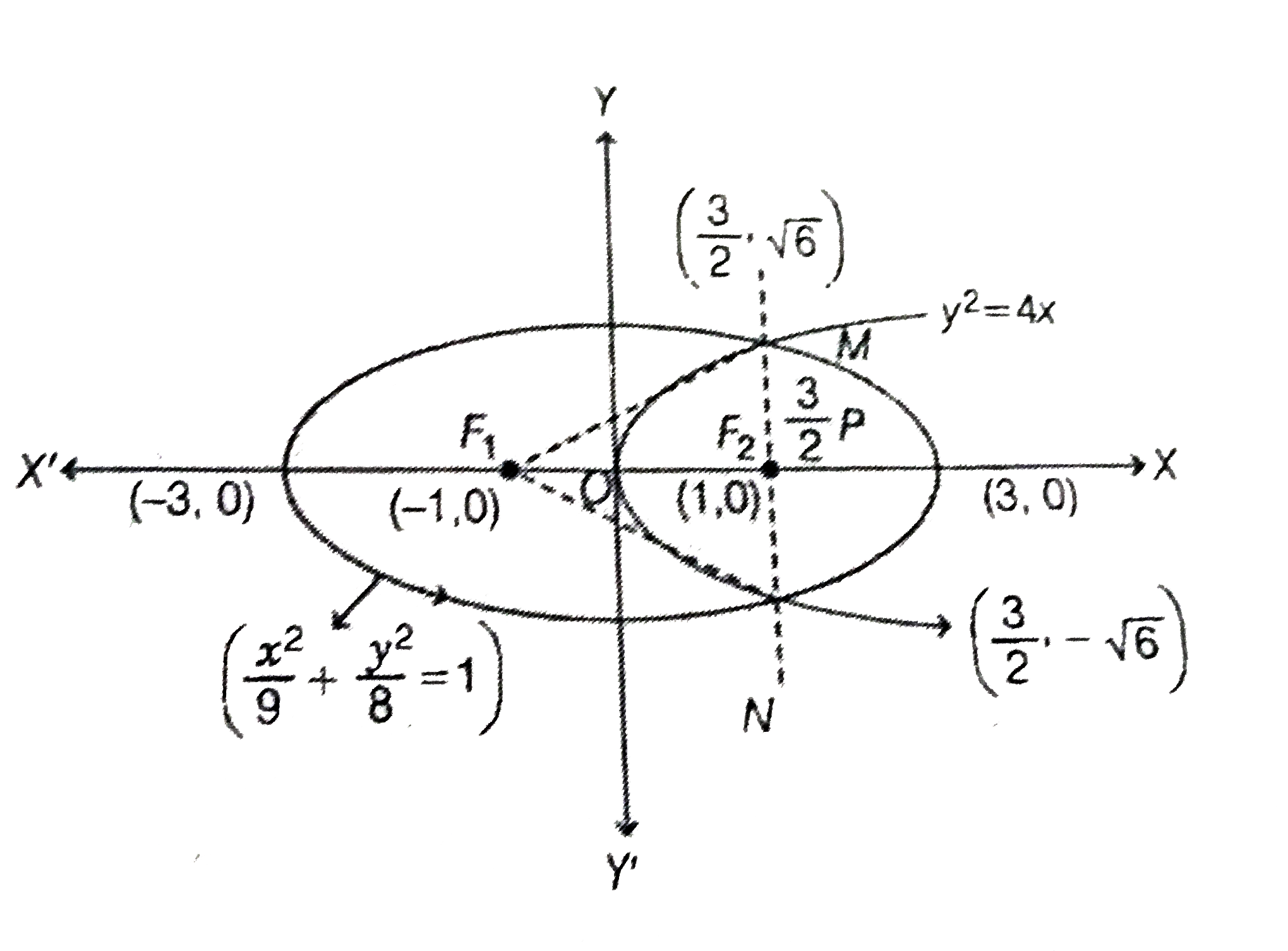
Equation of parabola having vertex O(0,0) and F2(1,0)(as,x2>0)
y2=4x
on solving x29+y28=1andy2=4x, we get
x=3/2andy=±√6
equation of altitude through M oin NF1 is
y−√6x−3/2=52√6
⇒(y−√6)=52√6(x−3/2). . .(iii)
and equilibrium of altitude through F1 is Y=0 . . .(iv)
on solving Eqs. (iii) and (iv) , we get (−910,0)as orthocentre.
Topper's Solved these Questions
- ELLIPSEBook:IIT JEE PREVIOUS YEARChapter:ELLIPSEExercise:EQUATION OF TANGENT AND NORMAL
Explore 23 Videos
- ELLIPSEBook:IIT JEE PREVIOUS YEARChapter:ELLIPSEExercise:EQUATION OF CHORD OF CONTACT, CHORD BISECTED AT A GIVEN POINT & DIAMETER
Explore 3 Videos
- DIFFERENTIAL EQUATIONS Book:IIT JEE PREVIOUS YEARChapter:DIFFERENTIAL EQUATIONS Exercise:TOPIC 3 APPLICATIONS OF HOMOGENEOUS DIFFERENTIAL EQUATIONS <br> ANALYTICAL & DESCRIPTIVE QUESTIONS
Explore 7 Videos
- FUNCTIONSBook:IIT JEE PREVIOUS YEARChapter:FUNCTIONSExercise:INVERSE AND PERIODIC FUNCTIONS
Explore 11 Videos
Similar Questions
Let F1(x1,0) and F2(x2,0), for x1<0 and x2>0, be the foci of the ellipse x29+y28=1 Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant. If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of area of the triangle MQR to area of the quadrilateral MF1NF2 is
View SolutionThe foci of the hyperbola 4x2−9y2−1=0 are
View Solution
Knowledge Check
Let F1(x1,0) and F2(x2,0), for x1<0 and x2>0, be the foci of the ellipse x29+y28=1 Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant. The orthocentre of the triangle F1MN is
A(−910,0)B(23,0)C(910,0)D(23,√6)If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of area of the triangle MQR to area of the quadrilateral MF1NF2 is
A(−910,0)B(23,0)C(910,0)D(23,√6)Let F1(x1,0) and F2(x2,0), for x1<0 andx2>0, be the foci of the ellipse x29+y28=1. Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant.
If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of the area of the triangle MQR to area of the quadrilateral MF1NF2 is :A3:4B4:5C5:8D2:3
Let F1(x1,0)andF2(x2,0) for x1<0andx2>0, be the foci of the ellipse x29+y28=1. Suppose a parabola having vertex at the origin and the focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrtant. Q. The eccentricity of an ellipse whose center is at the origin is 12. If one of its directices is x=−4, then the equation of the normal to its (1,32) is
View SolutionThe coordinate of foci of the hyperbola x29−y216=1 is
View SolutionThe foci of the hyperbola 4x2−9y2−1=0 are
View SolutionLet F1(x1,0)andF2(x2,0) for x1<0andx2>0 the foci of the ellipse x29+y28=1. Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at a point N in the fourth quardant. The orthocentre of the triangle F1MN, is
View SolutionThe foci of the hyperbola 4x2−9y2−1=0 are:
View Solution