Question

Area of the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$is $\pi ab$

Answer

A::B

Explanation

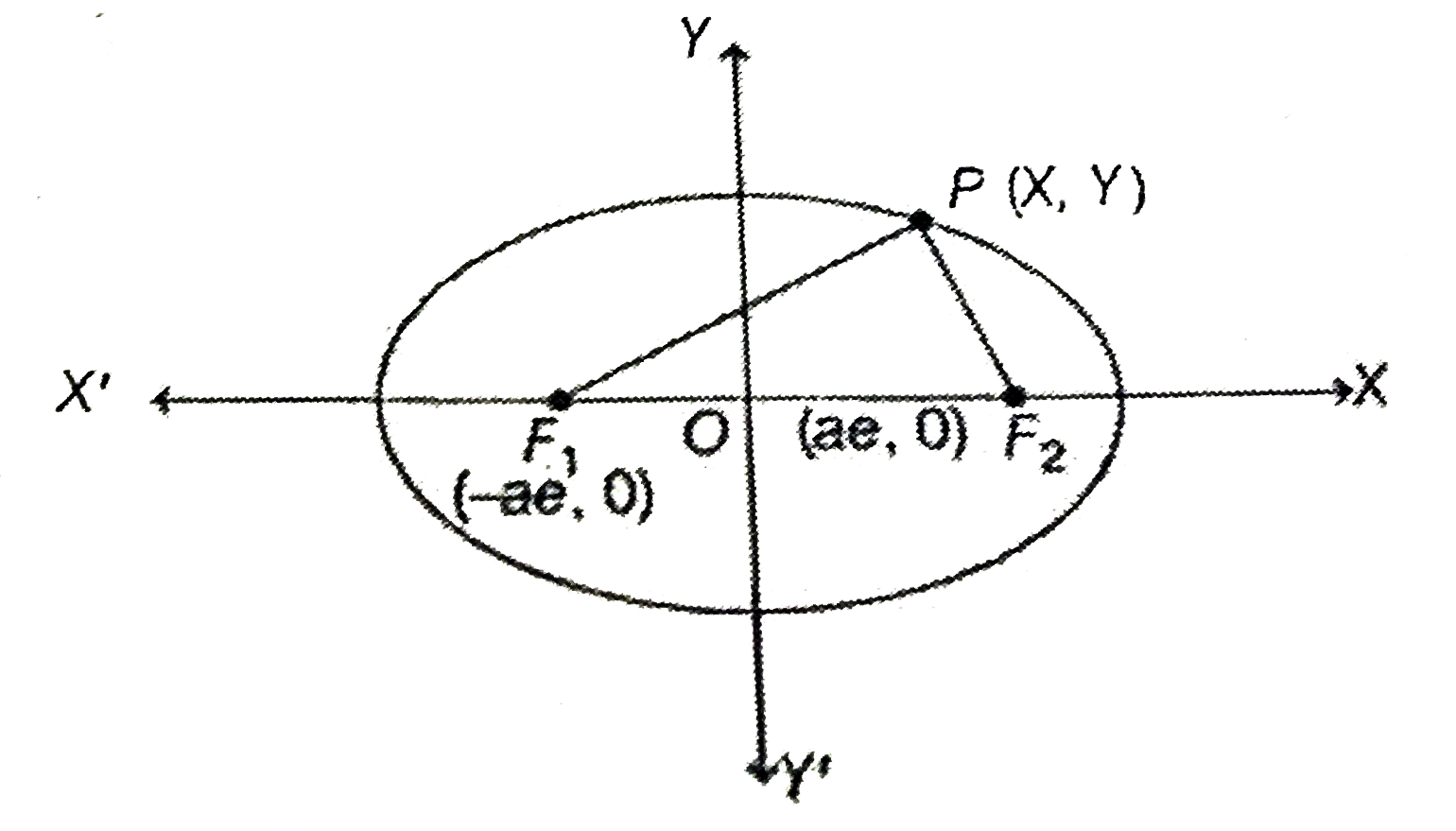
given , `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
Foci `F_(1) and f_(2)` are `(-ae,0) ` and (ae-0) respectively .Let p(x,y) be any variable point on the ellipse .
the area A of triangle `PF_(1)F_(2)` is given by

`A=(1)/(2) |{:(x,y,1),(-ae,0,1),(ae,0,1):}|`
`-(1)/(2)(-y)(-aexx1-aexx1)`
`=- (1)/(2) y-(-2ae)=a ey = ae.bsqrt(1-(x^(2))/(a^(2)))`
so A is maximum when x=0
`therefore ` Maximum of A `=abc=absqrt(1-(b^(2))/(a^(2))=absqrt(a^(3)-b^(2))/(a^(2))`
`= bsqrt(a^(2)-b^(2))`