Question

Consider
two straight lines, each of which is tangent to both the circle $x^2+y^2=\frac{1}{2}$
and the
parabola $y^2=4x$
. Let these
lines intersect at the point $Q$
. Consider
the ellipse whose center is at the origin $O(0,0)$
and whose
semi-major axis is $OQ$
. If the
length of the minor axis of this ellipse is $\sqrt{2}$
, then
which of the following statement(s) is (are) TRUE?
For the
ellipse, the eccentricity is $\frac{1}{\sqrt{2}}$
and the
length of the latus rectum is 1
(b) For the
ellipse, the eccentricity is $\frac{1}{2}$
and the
length of the latus rectum is $\frac{1}{2}$

(c) The
area of the region bounded by the ellipse between the lines $x=\frac{1}{\sqrt{2}}$
and $x=1$
is $\frac{1}{4\sqrt{2}}(\pi -2)$

(d) The
area of the region bounded by the ellipse between the lines $x=\frac{1}{\sqrt{2}}$
and $x=1$
is $\frac{1}{16}(\pi -2)$

Options

A. for the ellipse , the eccentricity is `1//sqrt(2)` and the length of the latus rectum is 1.
B. for the ellipse , the eccentricity is `1//2` and the length of the Latus is 1//2
C. the area of the region bounded by the ellipse between the lines `x=(1)/(2) and X=1 " is " (1) /(4sqrt(2))(pi-2)`
D. the area of the region bounded by the ellipse between the lines `x=(1)/(sqrt(2)) and x=1 " is " (1) /(16) (pi-2)`

Answer

A::C

Explanation

we have ,
equation of circle `x^(2)+y^(2)=(1)/(2)`
and Equation of Parabola `y^(2)=4`

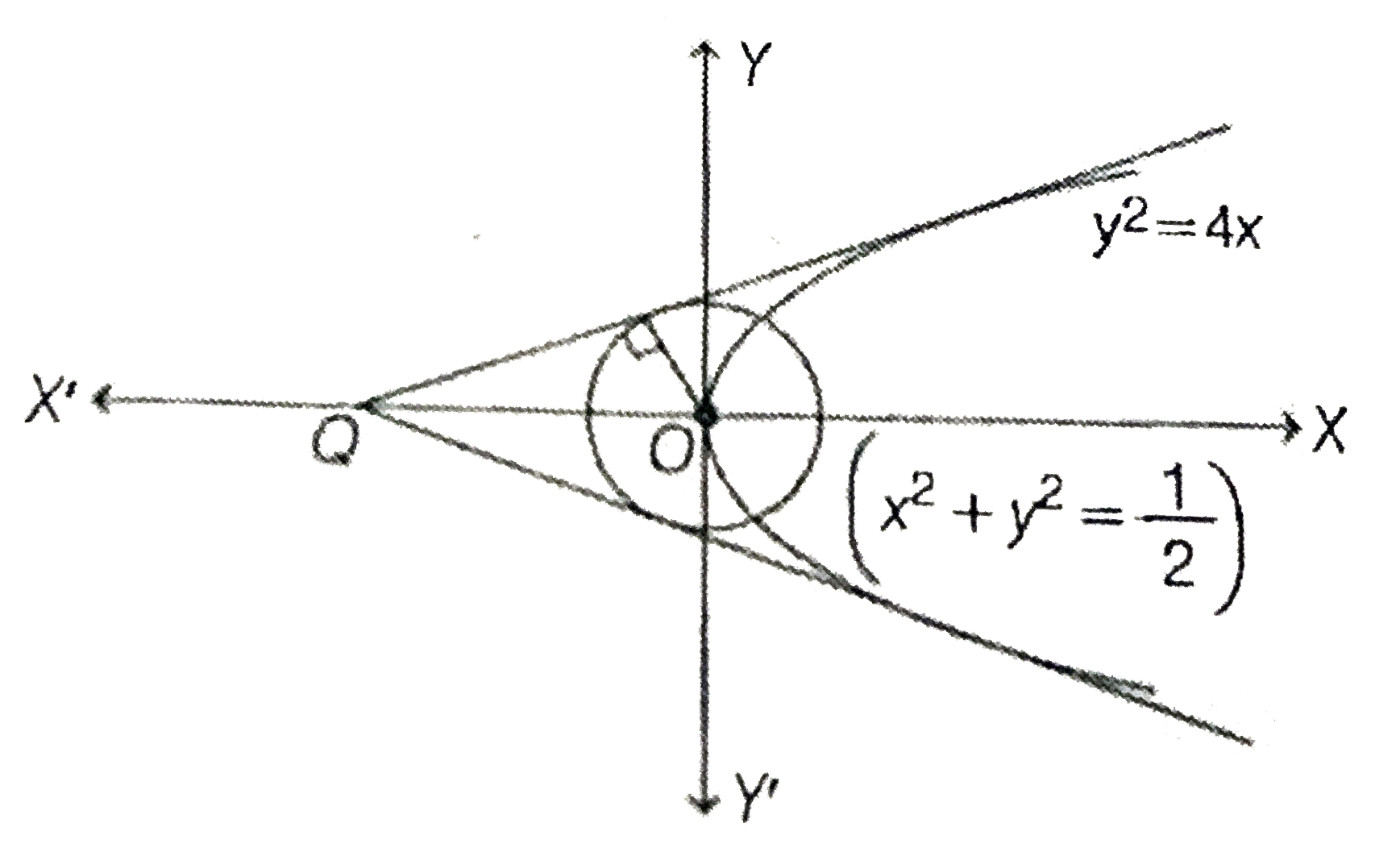
let the equation of common tangent of porabola and circle is
`y=mx+(1)/(m)`
since , radius of circle `=(1)/(sqrt(2))`
`therefore (1) /(sqrt(2))=|(0+0+(1)/(m))/(sqrt(1+m^(2)))|`
`impliesm^(4)+m^(2)-2=0implies m=+-1`
`therefore `Equation of common tangent are
`y=x+1and y=-x=1`
intesection point of common tangent at `q(-1,0) `
`therefore ` Equation of ellipse `(x^(2))/(1)+(y^(2))/(1//2)=1`
where, `a^(2)= 1,b^(2)=1//2`
Now, ecccentricity `(e) =sqrt(1-(b^(2))/(a^(2)))=sqrt(1-(1)/(2))=(1)/(sqrt(2))`
and length of latusrectum `=(2b^(2))/(a) =(2((1)/(2)))/(1)=1`

`therefore ` Area of shaded region
`=2 int_(1//sqrt(2))^(1)(1)/(sqrt(2))sqrt(1-x^(2))dx`
`= sqrt(2) [ (x)/(2) sqrt(1-x^(2))+(1)/(2) sin ^(-1)x]_(1//sqrt(2))^(1)`
`= sqrt(2)((pi)/(8)-(1)/(4))=(pi-2)/(4sqrt(2))`