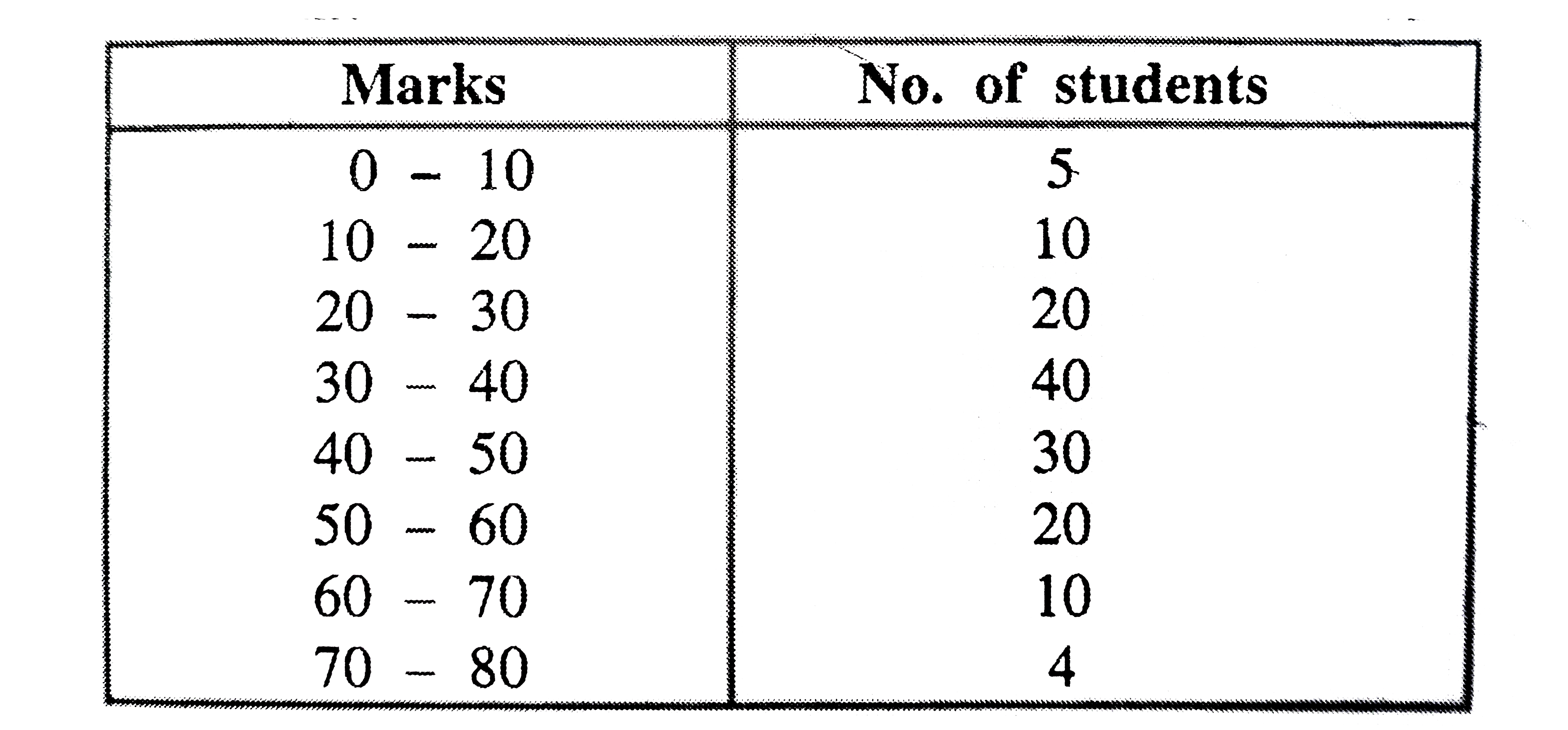
For a given distribution of marks mean is 35.16 and its standard deviation is 19.76. The coefficient of variation is :
19.7635.16×10
35.1619.76×100
19.7635.16
None of these
The correct Answer is:D
To find the coefficient of variation (CV) for the given distribution of marks, we can follow these steps:
Step 1: Understand the formula for Coefficient of Variation
The coefficient of variation (CV) is calculated using the formula:
CV=(Standard DeviationMean)×100
Step 2: Identify the given values
From the problem, we have:
- Mean (μ) = 35.16
- Standard Deviation (σ) = 19.76
Step 3: Substitute the values into the formula
Now, we will substitute the given values into the CV formula:
CV=(19.7635.16)×100
Step 4: Calculate the fraction
First, calculate the fraction:
19.7635.16≈0.561
Step 5: Multiply by 100
Now, multiply the result by 100 to get the coefficient of variation:
CV≈0.561×100≈56.1
Final Answer
Thus, the coefficient of variation is approximately 56.1%.
---
The coefficient of variation (CV) is calculated using the formula:
CV=(Standard DeviationMean)×100
From the problem, we have:
- Mean (μ) = 35.16
- Standard Deviation (σ) = 19.76
Now, we will substitute the given values into the CV formula:
CV=(19.7635.16)×100
First, calculate the fraction:
19.7635.16≈0.561
Now, multiply the result by 100 to get the coefficient of variation:
CV≈0.561×100≈56.1
Thus, the coefficient of variation is approximately 56.1%.
Topper's Solved these Questions
- STATISTICSBook:MODERN PUBLICATIONChapter:STATISTICSExercise:Objective B(Fill in the Blanks)
Explore 6 Videos
- STATISTICSBook:MODERN PUBLICATIONChapter:STATISTICSExercise:Objective C(True/False)
Explore 3 Videos
- STATISTICSBook:MODERN PUBLICATIONChapter:STATISTICSExercise:Exercise 15(c ) (Long Answer Type Question - I)
Explore 8 Videos
- SETS Book:MODERN PUBLICATIONChapter:SETS Exercise:CHAPTER TEST 1
Explore 12 Videos
- STRAIGHT LINES Book:MODERN PUBLICATIONChapter:STRAIGHT LINES Exercise:Chapter test
Explore 12 Videos
Similar Questions
Knowledge Check
The standard deviation (σ) of variate x is the square root of the A.M. of the squares of all deviations of x from the A.M. observations.
If xi/fi, i=1,2,… n is a frequency distribution then σ=√1NΣni=1fi(xi−¯x)2,N=Σni=1fi and variance is the square of standard deviation. Coefficient of dispersion is σx and coefficient of variation is σx×100
For a given distribution of marks mean is 35.16 and its standard deviation is 19.76 then coefficient of variation isA1.778B0.562C177.8D56.2For a given distribution of marks, the mean is 35.16 and its standard deviation is 19.76. The coefficient of variation is
A35.1619.76B19.7635.16C35.1619.76×100D19.7635.16×100The Binomial distribution whose mean is 3 and whose standard deviation is 3/2 is
A(1/2+1/2)12B(1/4+3/4)12C(3/4+1/4)12Dnone
For a Binomial Distribution, mean is 16 and standard deviation is 2, then q is
View SolutionFind out standard deviation and its coefficient of the following series:
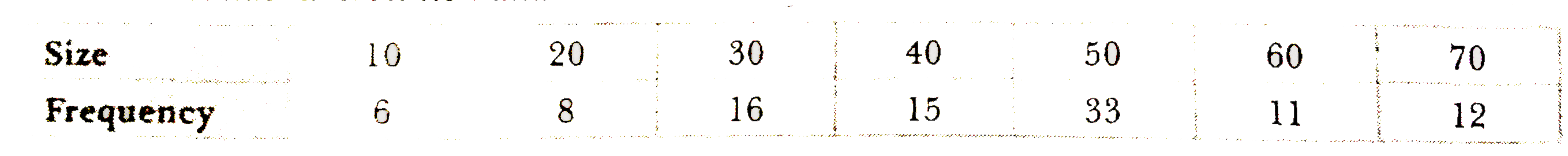
View SolutionThe mean of a distribution is 18 and the standard deviation is 4.5. What is the value of the coefficient of variation?
A. 50% B. 25% C. 100% D. 75%
View SolutionCoefficient of standard deviation is:
View SolutionThe mean of a distribution is 15 and the standard deviation is 5 . What is the value of coefficient variation ?
View Solution