If ¯x is the mean and mean deviation from mean is MD (¯x) , then find the number of observations lying between ¯x−MD(¯x) and ¯x+MD(¯x) from the following data :
34,66,30,38,44,50,40,60,42,51
The correct Answer is:6
To solve the problem, we will follow these steps:
Step 1: Calculate the Mean (x̄)
To find the mean, we sum all the observations and divide by the number of observations.
Given data:
34, 66, 30, 38, 44, 50, 40, 60, 42, 51
Calculation:
Mean(xˉ)=34+66+30+38+44+50+40+60+42+5110
=34+66+30+38+44+50+40+60+42+5110=40510=45.5
Step 2: Calculate the Mean Deviation (MD)
The mean deviation is calculated using the formula:
MD=∑|xi−xˉ|n
where xi are the observations, xˉ is the mean, and n is the number of observations.
Calculating the absolute deviations:
- For each observation, calculate |xi−xˉ|:
- For 34: |34−45.5|=11.5
- For 66: |66−45.5|=20.5
- For 30: |30−45.5|=15.5
- For 38: |38−45.5|=7.5
- For 44: |44−45.5|=1.5
- For 50: |50−45.5|=4.5
- For 40: |40−45.5|=5.5
- For 60: |60−45.5|=14.5
- For 42: |42−45.5|=3.5
- For 51: |51−45.5|=5.5
Sum of absolute deviations:
∑|xi−xˉ|=11.5+20.5+15.5+7.5+1.5+4.5+5.5+14.5+3.5+5.5=90
Mean Deviation Calculation:
MD=9010=9
Step 3: Calculate the Range
Now, we need to find the range between xˉ−MD and xˉ+MD.
Calculation:
xˉ−MD=45.5−9=36.5
xˉ+MD=45.5+9=54.5
Step 4: Count the Observations in the Range
Now we need to count how many observations lie between 36.5 and 54.5.
Observations:
- 34 (not in range)
- 66 (not in range)
- 30 (not in range)
- 38 (in range)
- 44 (in range)
- 50 (in range)
- 40 (in range)
- 60 (not in range)
- 42 (in range)
- 51 (in range)
Counting:
The observations that lie between 36.5 and 54.5 are: 38, 44, 50, 40, 42, and 51.
Total observations in range: 6
Final Answer
The number of observations lying between xˉ−MD and xˉ+MD is 6.
---
To find the mean, we sum all the observations and divide by the number of observations.
34, 66, 30, 38, 44, 50, 40, 60, 42, 51
Mean(xˉ)=34+66+30+38+44+50+40+60+42+5110
=34+66+30+38+44+50+40+60+42+5110=40510=45.5
The mean deviation is calculated using the formula:
MD=∑|xi−xˉ|n
where xi are the observations, xˉ is the mean, and n is the number of observations.
- For each observation, calculate |xi−xˉ|:
- For 34: |34−45.5|=11.5
- For 66: |66−45.5|=20.5
- For 30: |30−45.5|=15.5
- For 38: |38−45.5|=7.5
- For 44: |44−45.5|=1.5
- For 50: |50−45.5|=4.5
- For 40: |40−45.5|=5.5
- For 60: |60−45.5|=14.5
- For 42: |42−45.5|=3.5
- For 51: |51−45.5|=5.5
∑|xi−xˉ|=11.5+20.5+15.5+7.5+1.5+4.5+5.5+14.5+3.5+5.5=90
MD=9010=9
Now, we need to find the range between xˉ−MD and xˉ+MD.
xˉ−MD=45.5−9=36.5
xˉ+MD=45.5+9=54.5
Now we need to count how many observations lie between 36.5 and 54.5.
- 34 (not in range)
- 66 (not in range)
- 30 (not in range)
- 38 (in range)
- 44 (in range)
- 50 (in range)
- 40 (in range)
- 60 (not in range)
- 42 (in range)
- 51 (in range)
The observations that lie between 36.5 and 54.5 are: 38, 44, 50, 40, 42, and 51.
The number of observations lying between xˉ−MD and xˉ+MD is 6.
Topper's Solved these Questions
- STATISTICSBook:MODERN PUBLICATIONChapter:STATISTICSExercise:Exercise 15(b)(Short Answer Type Questions)
Explore 4 Videos
- STATISTICSBook:MODERN PUBLICATIONChapter:STATISTICSExercise:Exercise 15( c) (Short Answer Type Questions)
Explore 1 Video
- STATISTICSBook:MODERN PUBLICATIONChapter:STATISTICSExercise:Exercise 15(a) (Long Answer Type Questions- I)
Explore 6 Videos
- SETS Book:MODERN PUBLICATIONChapter:SETS Exercise:CHAPTER TEST 1
Explore 12 Videos
- STRAIGHT LINES Book:MODERN PUBLICATIONChapter:STRAIGHT LINES Exercise:Chapter test
Explore 12 Videos
Similar Questions
If ¯x is the mean and Mean Deviation from mean is MD (¯x), then find the number of observations lying between ¯x−MD(¯x) and ¯x+MD(¯x) from the following data :
22,24,30,27,29,31,25,28,41,42
View SolutionCalculate the mean deviation about median of the following data.(i) 34, 66, 30, 38, 44, 50, 40, 60, 42, 51
View Solution
Knowledge Check
Find the mean deviation from the median of the following data
 A7.08B7C7.1D7.05
A7.08B7C7.1D7.05If the sum of the deviations of 50 observations from 30 is 50, then the mean of these observations is
A50B51C30D31
Find the mean deviation using meadian from the following data:
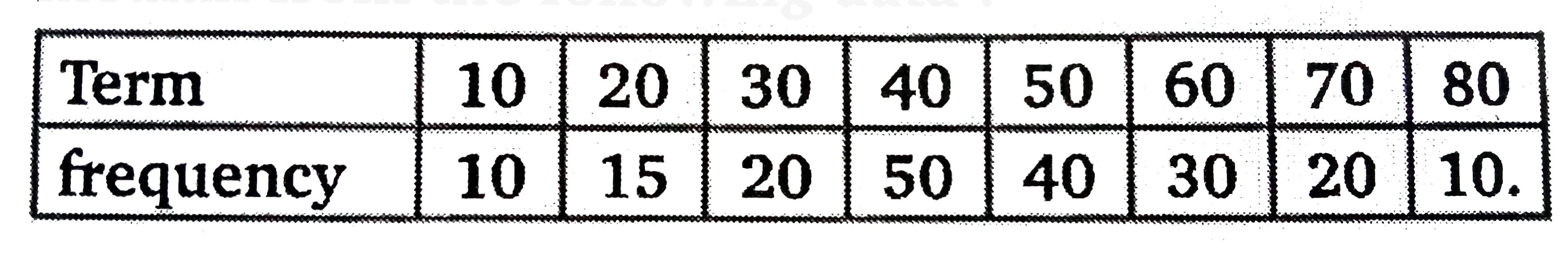
View SolutionFind the mean deviation from median for the following data :
36,72,46,42,60,45,53,46,51,49
View SolutionFind the mean deviation about the median for the following data :
34,23,46,37,40,28,32,50,35,44
View SolutionFind the mean deviation from the mean for the following data :
6,7,10,12,13,4,8,12
View SolutionFind the mean deviation from the mean for the following data :
4,7,8,9,10,12,13,17
View SolutionFind the mean deviation from the median for the following data :
38,70,48,34,63,42,55,44,53,47
View Solution

