The graph of x=5 is :
x - axis
y - axis
A line parallel to x - axis
A line parallel to y - axis.
The correct Answer is:D
To graph the equation x=5, we can follow these steps:
Step 1: Understand the Equation
The equation x=5 indicates that for any value of y, the value of x will always be 5. This means that the line will be vertical.
Hint: Remember that in the equation x=a, the line is vertical and crosses the x-axis at the point (a,0).
Step 2: Draw the Coordinate Axes
Start by drawing the x-axis (horizontal) and the y-axis (vertical) on a graph paper or a coordinate plane. Label the axes.
Hint: Make sure to label the axes clearly to avoid confusion when plotting points.
Step 3: Mark the Point on the X-Axis
Locate the point where x=5 on the x-axis. This point is (5,0).
Hint: You can find this point by moving 5 units to the right from the origin (0,0) along the x-axis.
Step 4: Draw the Vertical Line
Since x=5 is true for all values of y, draw a vertical line that passes through the point (5,0). This line should extend infinitely in both the upward and downward directions.
Hint: Use a ruler to ensure that the line is straight and extends clearly in both directions.
Step 5: Label the Line
Label the line as x=5 to indicate what the line represents.
Hint: Adding labels helps in identifying the equations of the lines on the graph.
Final Graph
You should now have a vertical line that crosses the x-axis at (5,0) and extends infinitely in both directions along the y-axis.
---
The equation x=5 indicates that for any value of y, the value of x will always be 5. This means that the line will be vertical.
Start by drawing the x-axis (horizontal) and the y-axis (vertical) on a graph paper or a coordinate plane. Label the axes.
Locate the point where x=5 on the x-axis. This point is (5,0).
Since x=5 is true for all values of y, draw a vertical line that passes through the point (5,0). This line should extend infinitely in both the upward and downward directions.
Label the line as x=5 to indicate what the line represents.
You should now have a vertical line that crosses the x-axis at (5,0) and extends infinitely in both directions along the y-axis.
Topper's Solved these Questions
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBook:MBD -HARYANA BOARDChapter:PAIR OF LINEAR EQUATIONS IN TWO VARIABLESExercise:SHORT ANSWER TYPE QUESTIONS
Explore 20 Videos
- MBD NEW STYPE MODEL TEST PAPER - 2Book:MBD -HARYANA BOARDChapter:MBD NEW STYPE MODEL TEST PAPER - 2Exercise:SET - D (SECTION - D)
Explore 6 Videos
- POLYNOMIALSBook:MBD -HARYANA BOARDChapter:POLYNOMIALSExercise:SHORT ANSWER TYPE QUESTIONS
Explore 16 Videos
Similar Questions
Knowledge Check
The graph of y=5 is a line
Amaking an intercept 5 on the x−axisBmaking an intercept 5 on the y− axisCparallel to the x−axis at a distance of 5 units from the originDparallel to the y−axis at a distance fo 5 units from the originGraph of x=5 is a line
AParallel to x-axisBParallel to y-axisCPasses through originDLying on x-axisThe total area (in sq. unit) of the triangles formed by the graph of 4x+5y=40,x− axis , y - axis and x = 5 and y = 4 is
A10B20C30D40
The graph of 2x=5−3y cuts the x-axis at the point P(α,β). The value of (2α+β) is :
View SolutionThe graph of 2x = 5-3y cuts the x-axis at the point P(α,β). The value of (2α+β) is
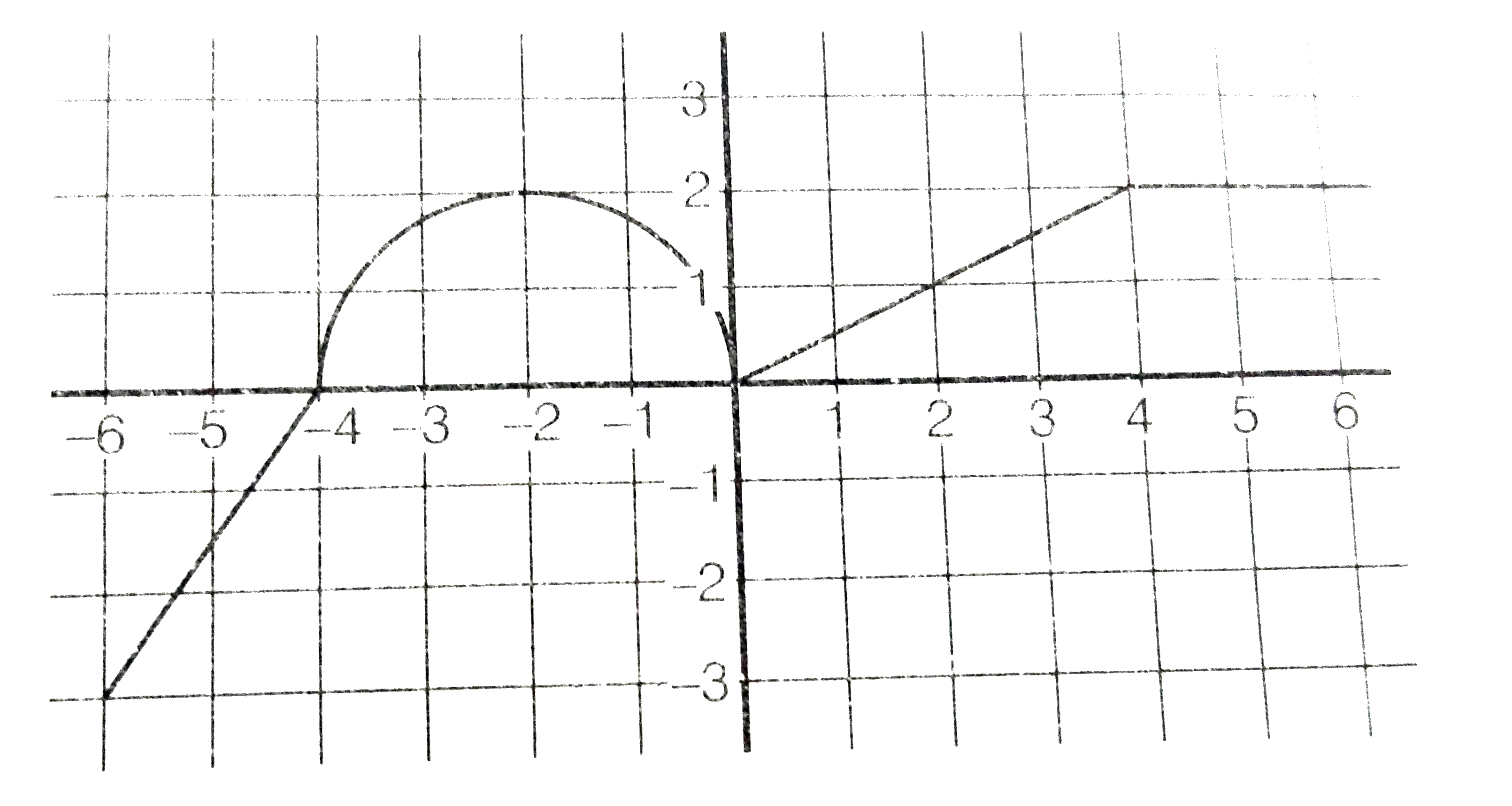
View SolutionThe graph y = f (x) is as shown:
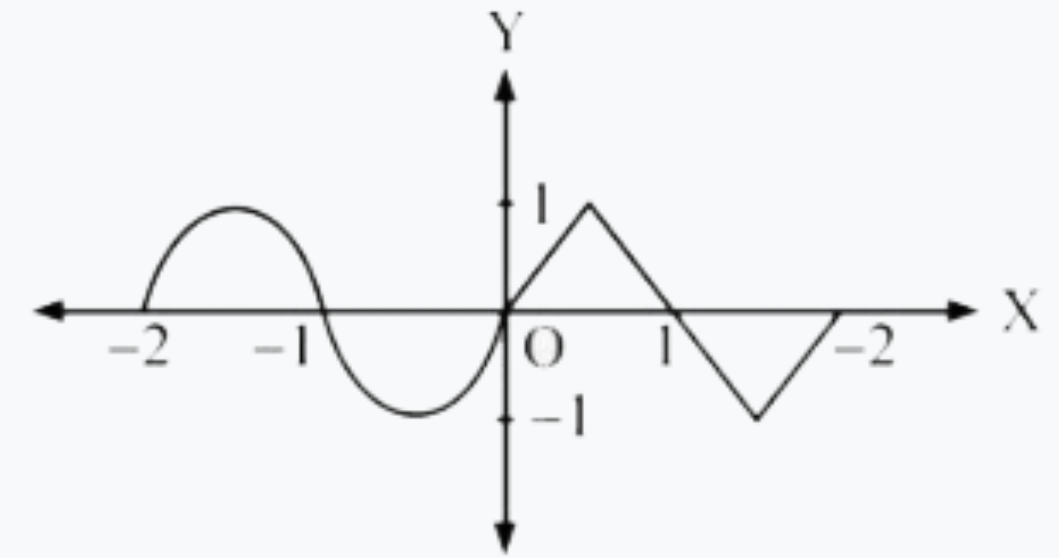
The graph of y = f (–|x|) is:
View SolutionGraph of |x| is
View SolutionSketch the graph of y=|x−5|. Evaluate ∫10|x−5|dx. What does this value of the integral represent on the graph.
View Solution