If t2andt3 of a GP are pandq, respectively, then t5=__________.
A
p(qp)3
B
p(qp)2
C
p2q3
D
p2q2
Video Solution
Text Solution
The correct Answer is:A
t2=ar=p
t3=ar2=q
⇒t3t2=qp=ar2ar⇒r=qp
ar=p
⇒a⋅qp=p⇒a=p2q
t5=a⋅r4
=p2q(qp)4
=p2q×q4p4=q3p2=p(qp)3
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PROGRESSIONSEXERCISE - LEVEL 217videos
PROGRESSIONS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PERMUTATIONS AND COMBINATION EXERCISE - LEVEL 315videos
PERMUTATIONS AND COMBINATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - REMAINDER AND FACTOR THEOREMSEXERCISE - Level 310videos
REMAINDER AND FACTOR THEOREMS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the pth, qth and rth terms of a G.P. be respectively , a,b and c then the value of aq−r.br−p.cp−q is :
A0B1C-1Dnone of these - Question 2 - Select One
If p,q and r are simple propositions with truth values T,F and T , respectively, then the truth value of (~p∨q)∧~r→p is
ATBFalseCtrue if r is falseDtrue if q is true - Question 3 - Select One
If for a G.P., r=2 and S8=510, then : t3 =
A2B15C8D18
If the pth,qthand rthterms of a GP are a, b and c, respectively. Prove that aq−rbr−pcp−q=1.
View SolutionThe rth,sthandtth terms of a certain G.P. are R,SandT respectively, prove that Rs−t⋅St−r⋅Tr−s=1
View SolutionIf T1,T2,T8 of a certain GP be x−4,xkandx52 respectively then prove that k=4
View SolutionIf T1,T2,T8 of a certain GP be x−4,xkandx52 respectively then prove that k=24
View SolutionIn Fig. 5.55, l ||m and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b.
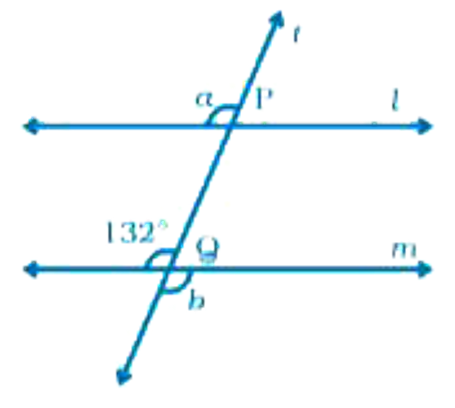 View Solution
View Solution

