The parallel sides of an isosceles trapezium PQRS are 12 cm and 6 cm and the distance between them is 4 cm. PT and QU are the perpendiculars drawn to SR. Find the area of the triangle PST (in cm2).
A
8
B
3
C
6
D
12
Video Solution
Text Solution
The correct Answer is:C
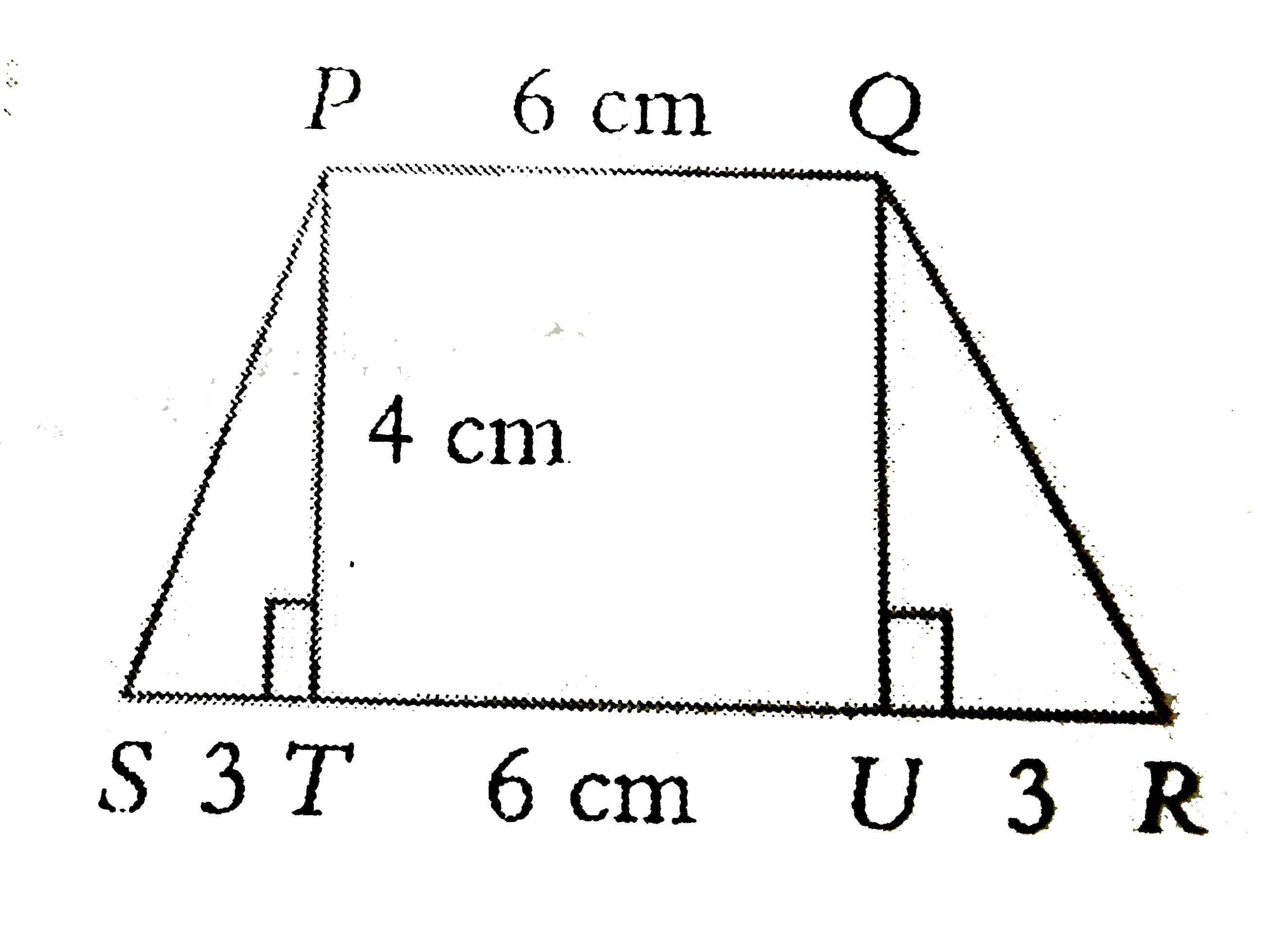
ST = UR
ST+UR+TU=12 cm (given)
2ST+PQ=12cm
2ST+6cm=12cm
2ST=6cm
ST=6cm2=3cm
PST is a right-angled triangle.
Area of triangle PST=12×ST×PT
=12×3×4=6cm2
|
Topper's Solved these Questions
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - ASSESSMENT TESTS
24 Videos
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Examples
13 Videos
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - CONCEPT APPLICATION (LEVEL 2)
38 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
- MOCK TESTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MOCK TESTEXERCISE - QUESTIONS
25 Videos
Similar Questions
Knowledge Check
The parallel sides of an isosceles trapezium PQRS are 12 cm and 6 cm and the distance between them is 4 cm. PT and QU are the perpendiculars drawn to SR. Find the area of the triangle PST (in cm2).
A8B3C6D12The parallel sides of a trapezium ABCD are 16 cm and 8 cm and the distance between them is 6 cm. AF and BE are the perpendiculars drawn to ¯¯¯¯¯¯DC. Find the total area of the triangles ADF and BCE (in cm2)
A36B24C30D28The parallel sides of a trapezium are 54 cm and 26 cm and the distance between them is 15 cm. The area of the trapezium is
A702cm2B810cm2C405cm2D600cm2
Two parallel sides of a trapezium are of lengths 27 cm and 19 cm respectively. and the distance between them is 14 cm. Find the area of the trapezium.
View SolutionFind the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm.
View SolutionThe parallel sides of a trapezium are 9.7 cm and 6.3 cm , and the distance between them is 6.5 cm. The area of the trapezium is
View SolutionThe parallel sides of a trapezium measure 14 cm and 18 cm and the distance between them is 9 cm. The area of the trapezium is
View SolutionTwo parallelogram sides of a trapezium are 12 cm and 8 cm long and the distance between them is 6.5 cm. The area of the trapezium is
View Solution
