The rates of simple interest in two banks x and y are in the ratio of 10:8. Rajni wants to deposit his total savings in two banks in such a way that she receive equal half-yearly interest from both. She should deposit the savings in banks x and y in the ratio of
4:5
3:5
5:4
2:1
The correct Answer is:A
To solve the problem, we need to determine the ratio in which Rajni should deposit her savings in banks X and Y so that she receives equal half-yearly interest from both banks.
1. Understand the Interest Rates:
The rates of simple interest in banks X and Y are given in the ratio of 10:8.
Let's denote the rate of interest for bank X as Rx=10x and for bank Y as Ry=8y.
2. Set Up the Interest Formula:
The formula for simple interest (SI) is given by:
SI=P×R×T100
where P is the principal amount, R is the rate of interest, and T is the time period.
3. Define the Principal Amounts:
Let Px be the amount deposited in bank X and Py be the amount deposited in bank Y.
4. Calculate the Simple Interest for Both Banks:
- For bank X:
SIx=Px×Rx×T100=Px×10x×12100=Px×10x200
- For bank Y:
SIy=Py×Ry×T100=Py×8y×12100=Py×8y200
5. Set the Interests Equal:
Since Rajni wants to receive equal interest from both banks:
SIx=SIy
Therefore,
Px×10x200=Py×8y200
6. Simplify the Equation:
We can cancel out the common factor of 200:
Px×10x=Py×8y
7. Express the Ratio of Principal Amounts:
Rearranging gives:
PxPy=8y10x=4y5x
8. Final Ratio:
Thus, the ratio in which Rajni should deposit her savings in banks X and Y is:
Px:Py=4y:5x
Conclusion:
Rajni should deposit her savings in banks X and Y in the ratio of 4y:5x.
The rates of simple interest in banks X and Y are given in the ratio of 10:8.
Let's denote the rate of interest for bank X as Rx=10x and for bank Y as Ry=8y.
The formula for simple interest (SI) is given by:
SI=P×R×T100
where P is the principal amount, R is the rate of interest, and T is the time period.
Let Px be the amount deposited in bank X and Py be the amount deposited in bank Y.
- For bank X:
SIx=Px×Rx×T100=Px×10x×12100=Px×10x200
- For bank Y:
SIy=Py×Ry×T100=Py×8y×12100=Py×8y200
Since Rajni wants to receive equal interest from both banks:
SIx=SIy
Therefore,
Px×10x200=Py×8y200
We can cancel out the common factor of 200:
Px×10x=Py×8y
Rearranging gives:
PxPy=8y10x=4y5x
Thus, the ratio in which Rajni should deposit her savings in banks X and Y is:
Px:Py=4y:5x
Rajni should deposit her savings in banks X and Y in the ratio of 4y:5x.
Topper's Solved these Questions
- SIMPLE INTERESTBOOK - ARIHANT SSCCHAPTER - SIMPLE INTERESTEXERCISE - (EXERCISE-C)(BASE LEVEL QUESTION)
43 Videos
- SIMPLE INTERESTBOOK - ARIHANT SSCCHAPTER - SIMPLE INTERESTEXERCISE - (EXERCISE-C)(HIGHER SKILL LEVEL QUESTION)
16 Videos
- SIMPLE INTERESTBOOK - ARIHANT SSCCHAPTER - SIMPLE INTERESTEXERCISE - (EXERCISE-C)(HIGHER SKILL LEVEL QUESTION)
16 Videos
- SIMPLE AND DECIMAL FRACTIONSBOOK - ARIHANT SSCCHAPTER - SIMPLE AND DECIMAL FRACTIONSEXERCISE - HIGHER SKILL LEVEL QUESTIONS
17 Videos
- SIMPLIFICATIONBOOK - ARIHANT SSCCHAPTER - SIMPLIFICATIONEXERCISE - HIGHER SKILL LEVEL QUESTIONS
21 Videos
Similar Questions
The rate of simple interest in two banks A and B are in the ratio 5:4 . A person wants to deposit his total savings in two banks in such a way that he received equal half-yearly interest from both. He should deposit the savings in the banks A and B in the ratio
View SolutionThe rates of simple interest in two banks A and B are in the ratio 5:4. A person wants to deposit his total savings in two banks sin such a way that he received equal half-yearly interest from both. He should deposit the savings in banks A and B in the ratio: (a) 2 : 5 (b) 4 : 5 (c) 5 : 2 (d) 5 : 4
View Solution
Knowledge Check
The rates of simple interest in two banks A and B are in the ratio 5:4. A person wants to deposit his total savings in two banks sin such a way that he received equal half-yearly interest from both. He should deposit the savings in banks A and B in the ratio: (a) 2 : 5 (b) 4 : 5 (c) 5 : 2 (d) 5 : 4
A5:2B2:5C4:5D5:4The rate of interest in two hanks DNB and HBI are in the ratio of 7: 8. If a person invested some amount in both the banks and received equal amounts from both the banks in two years. The ratio of amount invested in DNB and HBI, respectively is:
A15:1B8:7C7:8D108:107The rate of interest in two hanks DNB and HBI are in the ratio of 7: 8. If a person invested some amount in both the banks and received equal amounts from both the banks in two years. The ratio of amount invested in DNB and HBI, respectively is:
A15:1B8:7C7:8D108:107
Two different companies announces to invest money at in company at a particular interest rate of their investors. The interest rate announced by company and by bank of country can be different in different years. The yearly interest rate by two companies P and Q is shown in the graph
Study the graph and answer the question
The yearly interest rate of two companies P and Q in last few years.
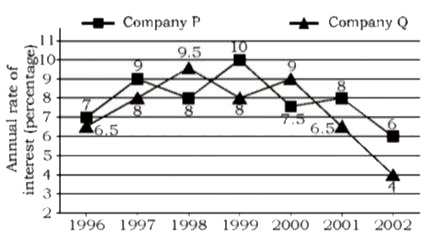
If in year 1999 two amounts in the ratio 9:10 was invested in company P and Q then the ratio of simple interest from P and Q after one year?
View SolutionRahi deposited ₹600 in a bank that promised 8% simple interest per annum. If Rahi kept the money with the bank for 5 years, she will earn an interest of :
View SolutionThe difference of simple interest from two banks for X 1000 in 2 yr is X 20. Find the difference in rates of interest.
View SolutionSunita divide a sum of money in 3 parts and deposit these in 3 different bank. The ratio the rate of interest is 4:6:3 of the banks respectively. If he receive the same interest from these banks after 9 months. Find the ratio of deposited sum.
View SolutionYour friend gets Rs 10,000 from his grand parent. He/she wants to invest in a bank in such a way he/she need not withdraw the amount partly or wholly for two years. What kind of account should he/she open in a bank?
View Solution
