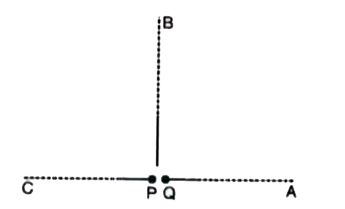
In the figure given below, P and Q are two equally intense coherent sources emitting radiations of wavelength 20 m. The separation between P and Q is 5.0 metre and phase of P is ahead of the phase of Q by 90∘, A, B and C are three distant points of observation, equidistant from the mid point of PQ.The intensity of radiation at A, B, and C will bear the ratio :
0:1:4
4:1:0
0:1:2
2:1:0
The correct Answer is:D
Let I be the intensity of each source.λ=20m

Path difference PQ = 5m = λ4
So phase difference = λ4×2πλ=π2.
Initial phase at P is π2 so, phase difference between P and Q w.r.t A is zero.
Net phase difference between P and Q w.r.t B = π2.
Net phase difference between P and Q w.r.t C=π2.
∴IA=I+I+2√I.Icos0∘=4I
IB=I+I+2√I.Icos90∘=2I
IC=I+I+2√I.Icos180∘=0
∴RatioIA:IB:IC::2:1:0
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - MCQ LEVEL -1 (ASSERTIONS)3videos
WAVE OPTICS
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - MCQ LEVEL -1 (PARAGRAPH QUESTIONS )34videos
WAVE OPTICS
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE MOTIONEXERCISE - RECENT COMPETITIVE QUESTIONS18videos
WAVE MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Revision Test40videos
WORK , POWER , ENERGY AND COLLISIONS
Similar Questions
Fig, here shows P and Q as two equally intense coherent sources emitting radiations of wavelength 20m. The separation PQ si 5m, and phase of P is ahead of the phase Q by 90∘. A, B and C are three distant points of observation equidistant from the mid - point of PQ. The intensity of radiations of A, B, C will be in the ratio
 View Solution
View SolutionFig, here shows P and Q as two equally intense coherent sources emitting radiations of wavelength 20m. The separation PQ si 5m, and phase of P is ahead of the phase Q by 90∘. A, B and C are three distant points of observation equidistant from the mid - point of PQ. The intensity of radiations of A, B, C will be in the ratio
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Fig, here shows P and Q as two equally intense coherent sources emitting radiations of wavelength 20m. The separation PQ si 5m, and phase of P is ahead of the phase Q by 90∘. A, B and C are three distant points ofobservation equidistant from the mid - point of PQ. The intensity of radiations of A, B, C will beasr the ratio
 A0:1:4B4:1:0C0:1:2D2:1:0
A0:1:4B4:1:0C0:1:2D2:1:0 - Question 2 - Select One
P and Q are points on the line joining A(-2,5) and B(3,1) such that AP=PQ=QB. Then the mid pont of PQ is
A(12,3)B(−12,4)C(2,3)D(1,4) - Question 3 - Select One or More
If the point P(p,q) is equidistant from the points A(a+b,b−a)andB(a−b,a+b), then
Aap=bqBaq=bpCp2−q2=2(ap+bp)DPcanbe(a,b)
If A(−2,50,B(3,1)andP,Q are the points of trisection of ¯¯¯¯¯¯AB, then mid point of ¯¯¯¯¯¯PQ is
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
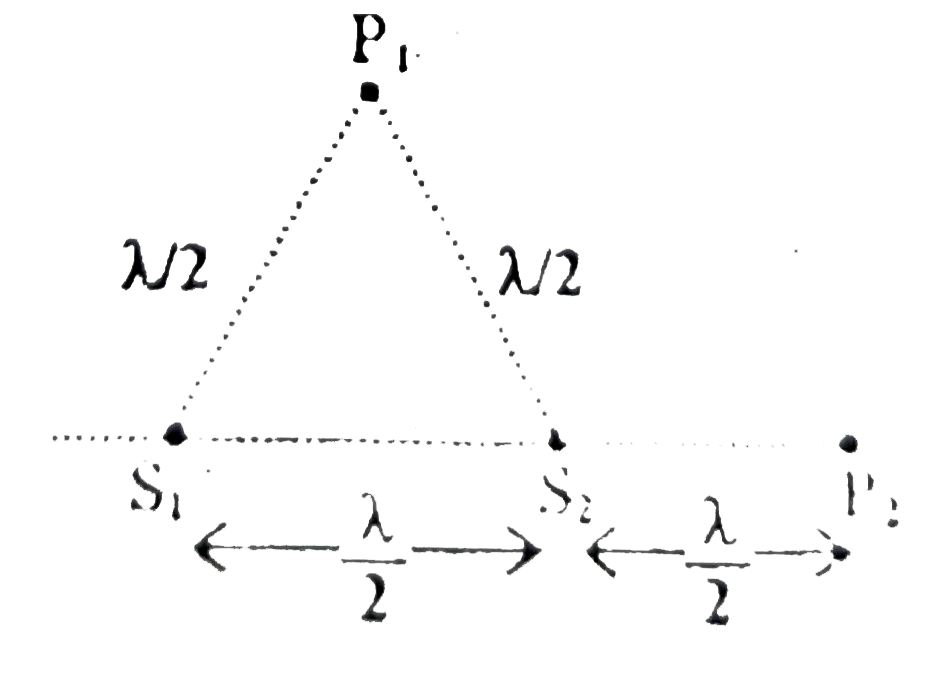 View Solution
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
 View Solution
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
 View Solution
View SolutionP and Q are points on the line joining A(-2,5) and B(3,1) such that AP=PQ=QB. Then the mid pont of PQ is
View Solution

