Find the value of x in the given figure.
The correct Answer is:−16 is not possible
To find the value of x in the given figure, we can use the Power of a Point theorem, which states that for a point P outside a circle, the product of the lengths of the segments of any secant line through P is equal to the product of the lengths of the segments of any other secant line through P.
1. Identify the segments:
- From the figure, we have the following segments:
- PC=8
- CA=4
- PD=7
- BD=x
2. Calculate PA:
- Since PA=PC+CA, we can calculate:
PA=8+4=12
3. Set up the equation using the Power of a Point theorem:
- According to the theorem:
PC×PA=PD×PB
- Here, PB=PD+BD=7+x.
- Plugging in the values, we get:
8×12=7×(7+x)
4. Calculate the left side:
- Calculate 8×12:
8×12=96
5. Set up the equation:
- Now we have:
96=7×(7+x)
6. Distribute on the right side:
- Distributing 7:
96=49+7x
7. Isolate 7x:
- Subtract 49 from both sides:
96−49=7x
47=7x
8. Solve for x:
- Divide both sides by 7:
x=477≈6.71
9. Final answer:
- Thus, the value of x is approximately 6.71.
- From the figure, we have the following segments:
- PC=8
- CA=4
- PD=7
- BD=x
- Since PA=PC+CA, we can calculate:
PA=8+4=12
- According to the theorem:
PC×PA=PD×PB
- Here, PB=PD+BD=7+x.
- Plugging in the values, we get:
8×12=7×(7+x)
- Calculate 8×12:
8×12=96
- Now we have:
96=7×(7+x)
- Distributing 7:
96=49+7x
- Subtract 49 from both sides:
96−49=7x
47=7x
- Divide both sides by 7:
x=477≈6.71
- Thus, the value of x is approximately 6.71.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - Fast Track Practice
104 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
What is the value of x in the given figure?
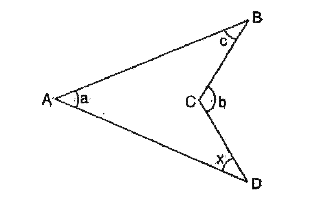 Ab−a−cBb−a+cCb+a−cD(a+b+c)
Ab−a−cBb−a+cCb+a−cD(a+b+c)Find x in the given figure.
 A13 cmB12 cmC16 cmD15 cm
A13 cmB12 cmC16 cmD15 cm
Find the value of ∠ABC in the given figure
View SolutionFind the value of x in the figure
View SolutionFind the value of x in the figure
View SolutionFind Value of x in the given figure:
View SolutionFind the value of x in the adjacent figure.
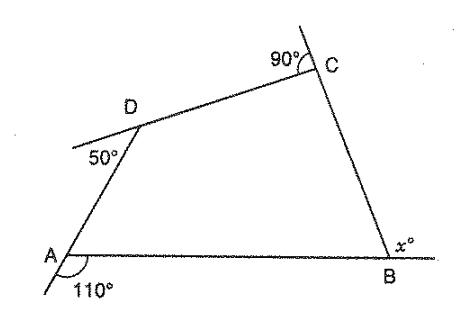
View SolutionFind the value of x in the adjoining figure.
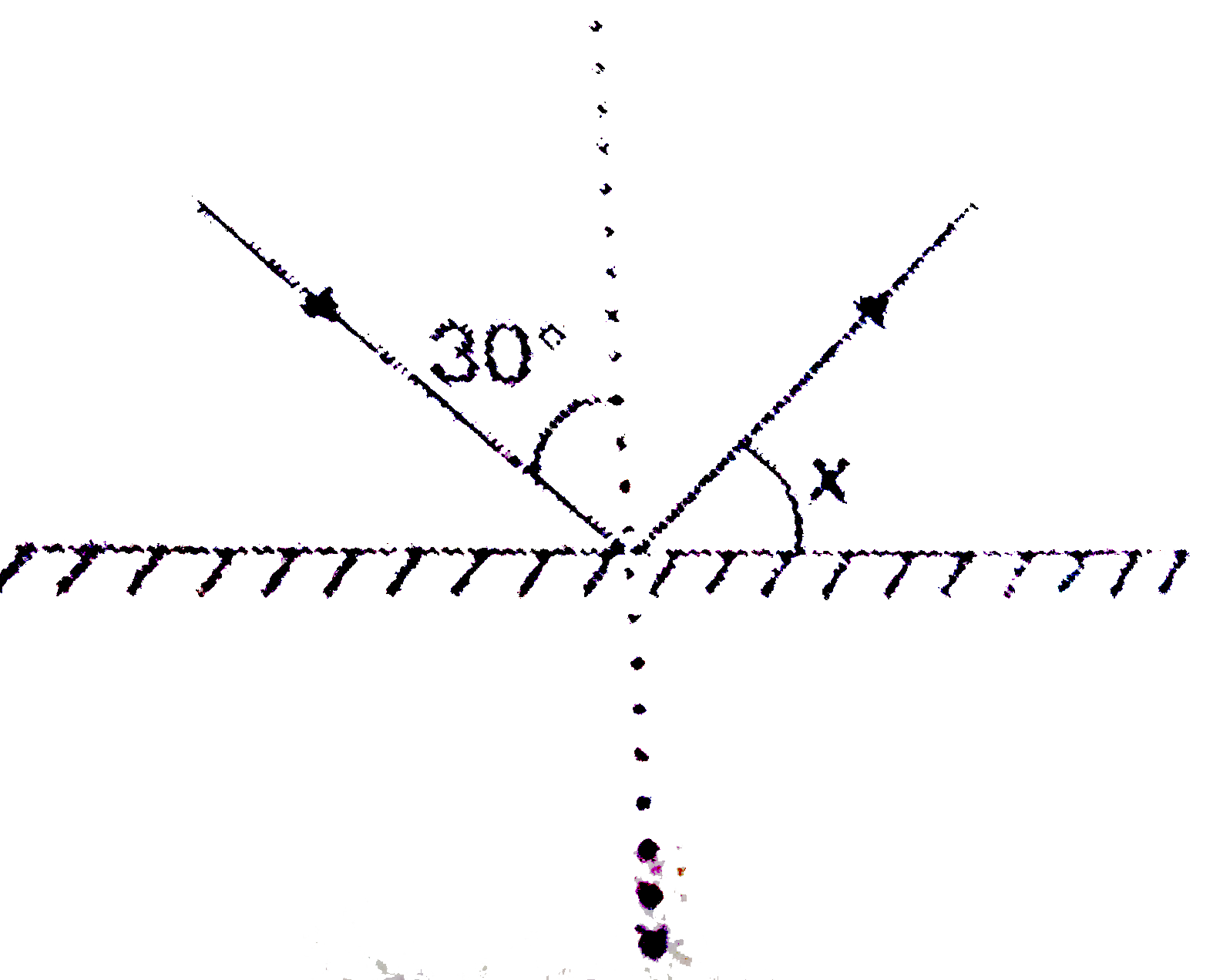
View Solution
