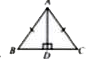
The area of an isosceles triangle ABC with AB=AC and altitude AD=3cm is 12sqcm. What is its perimeter?
18 cm
6 cm
14 cm
12 cm
The correct Answer is:A
To solve the problem step by step, we will follow the instructions given in the video transcript.
Step 1: Understand the given information
We have an isosceles triangle ABC where:
- AB=AC
- The altitude AD=3cm
- The area of triangle ABC is 12cm2
Step 2: Use the area formula for triangles
The area A of a triangle can be calculated using the formula:
A=12×base×height
In our case, the height (altitude) is AD=3cm and the area is 12cm2. We can set up the equation:
12=12×base×3
Step 3: Solve for the base
Rearranging the equation to find the base:
12=32×base
Multiplying both sides by 23:
base=12×23=243=8cm
Step 4: Identify the lengths of the sides
Since ABC is an isosceles triangle, we denote:
- AB=AC=x
- The base BC=8cm
Step 5: Apply the Pythagorean theorem
In triangle ABD (where D is the foot of the altitude from A to BC):
- BD=BC2=82=4cm
- AD=3cm
Using the Pythagorean theorem:
AB2=AD2+BD2
Substituting the known values:
x2=32+42
x2=9+16=25
Taking the square root:
x=√25=5cm
Thus, AB=AC=5cm.
Step 6: Calculate the perimeter
The perimeter P of triangle ABC is given by:
P=AB+AC+BC=5+5+8=18cm
Final Answer
The perimeter of triangle ABC is 18cm.
---
We have an isosceles triangle ABC where:
- AB=AC
- The altitude AD=3cm
- The area of triangle ABC is 12cm2
The area A of a triangle can be calculated using the formula:
A=12×base×height
In our case, the height (altitude) is AD=3cm and the area is 12cm2. We can set up the equation:
12=12×base×3
Rearranging the equation to find the base:
12=32×base
Multiplying both sides by 23:
base=12×23=243=8cm
Since ABC is an isosceles triangle, we denote:
- AB=AC=x
- The base BC=8cm
In triangle ABD (where D is the foot of the altitude from A to BC):
- BD=BC2=82=4cm
- AD=3cm
AB2=AD2+BD2
Substituting the known values:
x2=32+42
x2=9+16=25
Taking the square root:
x=√25=5cm
Thus, AB=AC=5cm.
The perimeter P of triangle ABC is given by:
P=AB+AC+BC=5+5+8=18cm
The perimeter of triangle ABC is 18cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
△ABC is an isosceles triangle with AB=AC=15cm and altitude from A to BC is 12 cm. The length of sides BC is :
A9 cmB12 cmC18 cmD20 cm - Question 2 - Select One
The base of an isosceles triangle measures 24 cm and its area is 192cm2 , Find its perimeter.
A4 cmB64 cmC32 cmD20 cm - Question 3 - Select One
The altitude of an equilateral triangle is √3cm. What is its perimeter?
A3 cmB3√3cmC6 cmD6a3cm
The base of an isosceles triangle is 12 cm and its perimeter is 32 cm. Find its area.
View SolutionThe base of an isosceles triangle is 12 cm and its perimeter is 32 cm. Find its area.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
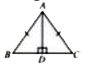
AD bisects ∠AView SolutionIn an isosceles triangle ABC with AB = AC and AD is perpendicular to BC, if AD = 6 cm and the perimeter of △ABC is 36 cm, then the area of △ABC is:
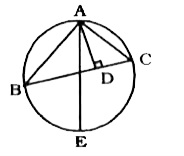
एक समद्विबाह त्रिभुज ABC में AB=AC और AD, BC पर लंबवत है, यदि AD = 6 सेमी और ABC की परिधि 36 सेमी है, तो ABC का क्षेत्रफल हैView SolutionIn the given figure, ABC is a triangle in which, AB=12cm,AC=6cmand altitude AD=4cm. If AEis the diameter of the circumcircle, than what is the length (in cm) of circum-radius?
 View Solution
View Solution