In an examination paper of five questions, 5% of the candidates answered all of them and 5% answered none. Of the rest, 25% candidates answered only one question and 20% answered 4 questions. If 396 candidates answered either 2 questions or 3 questions, the number of candidates that appeared for the examination was
800
1000
850
900
The correct Answer is:A
To solve the problem step by step, we will break down the information given and calculate the total number of candidates who appeared for the examination.
Step 1: Define the total number of candidates
Let the total number of candidates who appeared for the examination be A.
Step 2: Calculate the number of candidates who answered all questions
5% of the candidates answered all 5 questions. Therefore, the number of candidates who answered all questions is:
Candidates who answered all=5100×A=A20
Step 3: Calculate the number of candidates who answered none
Similarly, 5% of the candidates answered none of the questions. Therefore, the number of candidates who answered none is also:
Candidates who answered none=5100×A=A20
Step 4: Calculate the remaining candidates
The remaining candidates are those who answered either 1, 2, 3, or 4 questions. We can find this by subtracting the candidates who answered all and none from the total:
Remaining candidates=A−(A20+A20)=A−2A20=A−A10=9A10
Step 5: Calculate the number of candidates who answered only one question
25% of the remaining candidates answered only one question:
Candidates who answered only one=25100×9A10=9A40
Step 6: Calculate the number of candidates who answered four questions
20% of the remaining candidates answered four questions:
Candidates who answered four=20100×9A10=9A50
Step 7: Calculate the number of candidates who answered either 2 or 3 questions
We know that 396 candidates answered either 2 or 3 questions. Thus, we can express this as:
Candidates who answered 2 or 3=9A10−(9A40+9A50)
Step 8: Find a common denominator and simplify
To simplify 9A40+9A50, we find the LCM of 40 and 50, which is 200:
9A40=9A×5200=45A200
9A50=9A×4200=36A200
Thus,
9A40+9A50=45A+36A200=81A200
Step 9: Set up the equation
Now we can set up the equation for the candidates who answered either 2 or 3 questions:
9A10−81A200=396
Converting 9A10 to have a denominator of 200 gives:
9A×20200=180A200
Thus, the equation becomes:
180A200−81A200=396
99A200=396
Step 10: Solve for A
Now, multiply both sides by 200:
99A=396×200
99A=79200
Now, divide by 99:
A=7920099=800
Conclusion
The total number of candidates that appeared for the examination is 800.
Let the total number of candidates who appeared for the examination be A.
5% of the candidates answered all 5 questions. Therefore, the number of candidates who answered all questions is:
Candidates who answered all=5100×A=A20
Similarly, 5% of the candidates answered none of the questions. Therefore, the number of candidates who answered none is also:
Candidates who answered none=5100×A=A20
The remaining candidates are those who answered either 1, 2, 3, or 4 questions. We can find this by subtracting the candidates who answered all and none from the total:
Remaining candidates=A−(A20+A20)=A−2A20=A−A10=9A10
25% of the remaining candidates answered only one question:
Candidates who answered only one=25100×9A10=9A40
20% of the remaining candidates answered four questions:
Candidates who answered four=20100×9A10=9A50
We know that 396 candidates answered either 2 or 3 questions. Thus, we can express this as:
Candidates who answered 2 or 3=9A10−(9A40+9A50)
To simplify 9A40+9A50, we find the LCM of 40 and 50, which is 200:
9A40=9A×5200=45A200
9A50=9A×4200=36A200
Thus,
9A40+9A50=45A+36A200=81A200
Now we can set up the equation for the candidates who answered either 2 or 3 questions:
9A10−81A200=396
Converting 9A10 to have a denominator of 200 gives:
9A×20200=180A200
Thus, the equation becomes:
180A200−81A200=396
99A200=396
Now, multiply both sides by 200:
99A=396×200
99A=79200
Now, divide by 99:
A=7920099=800
The total number of candidates that appeared for the examination is 800.
Topper's Solved these Questions
Similar Questions
Five question were asked in an examination. 5% of the total examinees answered all 5 questions and 5% of total examinees did not answered any question. 25% of the rest of the examinees answered only 1 question and 20% answered 4 questions. 2412% of the total examinees answered only 2 questions. If 200 examinees answered 3 questions, then find the total number of examinees.
View SolutionIn an examination, 92% of the candidates passed and 46 failed. How many candidates appeared?
View Solution
Knowledge Check
In an examination, 60% of the candidates passed in English and 70% of the candidates passed in Mathematics, but 20% failed in both of these subjects. If 2500 candidates passed in both the subjects, the number of candidates that appeared at the examination was
A3000B3500C4000D5000In an examination, 60% of the candidates passed in English and 70% of the candidates passed in Mathematics, but 20% failed in both of these subjects. If 2500 candidates passed in both the subjects, the number of candi dates who appeared at the ex amination was
A3000B3500C4000D5000In an examination 74% of the candidates passed and 156 failed. The candidates who appeared in the examination were
A211B400C500D600
In an examination, 94% of the candidates passed and 114 failed. How many candidates appeared?
View SolutionIn an examination 75% candidates mas in English and 60% passed in Mathematics. 25% failed in both and 240 passed the examination. Find the total number of candidates
View Solutionin an examination 96% of the candidate passed and 50 failed. how many candidate appeared?
View SolutionIn an examination 70% of the candidates passed in English, 80% passed in Mathematics. 10% failed in both the subjects if 144 candidates passed in both, the total number of candidates was :
एक परीक्षा में 70% प्रतियोगी अंग्रेजी में, 80% प्रतियोगी गणित में सफल होते है तथा 10% प्रतियोगी दोनों विषयों में असफल होते हैं। यदि 144 प्रतियोगी दोनों विषयों में सफल होते हैं, तो प्रतियोगियों की कुल संख्या क्या थी ?
View SolutionStudy the following graph carefully and answer the question given below
Number of candidates appeared (in thousand) and percentage of candidates qualified in a competitive examination over the years.
No. of candidates appeared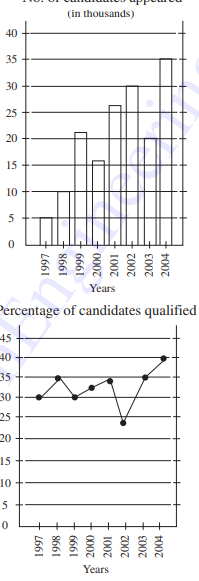
What was the percentage drop in thee number of candidates appeared from the year 2002 to 2003?
View Solution
