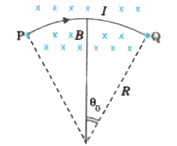
A wire carrying current I is tied between points P and Q and is in the shape of a circular arch of radius R due to a uniform magnetic field B (perpendicular to the plane of the paper, shown by cross marked) in the vicinity of the wire. If the wire subtends and angle 2θ0 at the centre of the circle of which it forms an arch) then the tension in the wire is:
IBR
IBRsinθ0
IBR2sinθ0
IBRθ0sinθ0
The correct Answer is:a
Net magnetic force on wire inside uniform magnetic field depends on the direct distance between two ends of wire. Let Fm . be the magnetic force on given section of wire and be the tension Tension acts along the tangent to the circular arc as shown in figure.
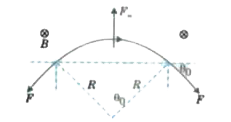
For wire to remain in equilibrium we can write the following equation.
2Fsinθ0=Fm
2Fsinθ0=i(2Rsinθ)B
⇒ F=iRB
Hence option (a) is correct.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
28 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (A. MULTIPLE CHOICE QUESTIONS)
38 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
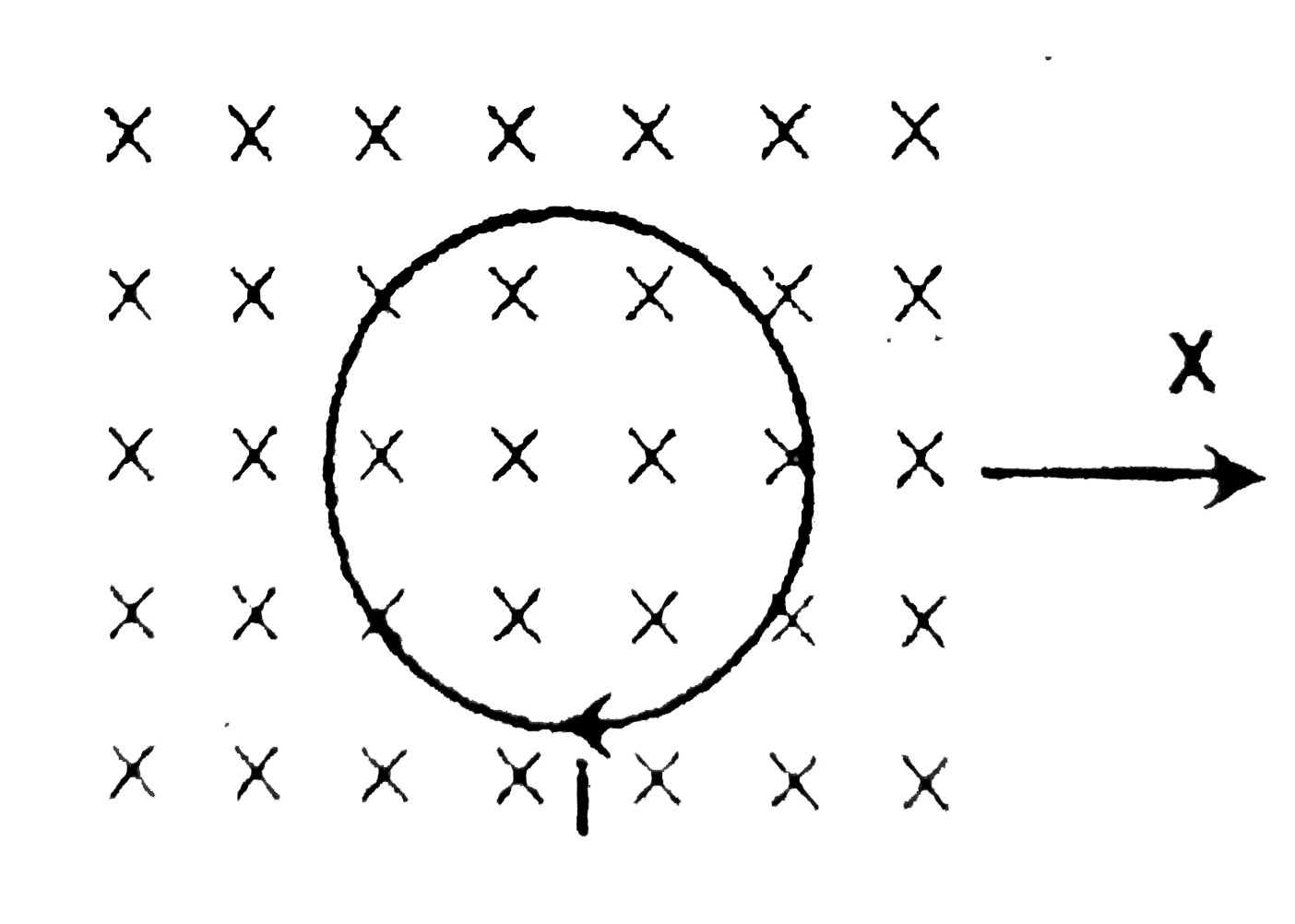
A circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View Solution
Knowledge Check
A current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
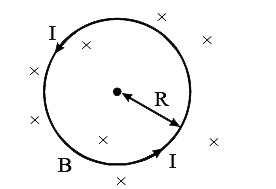 ABIRB2πBIRCπBIRD2BIR
ABIRB2πBIRCπBIRD2BIR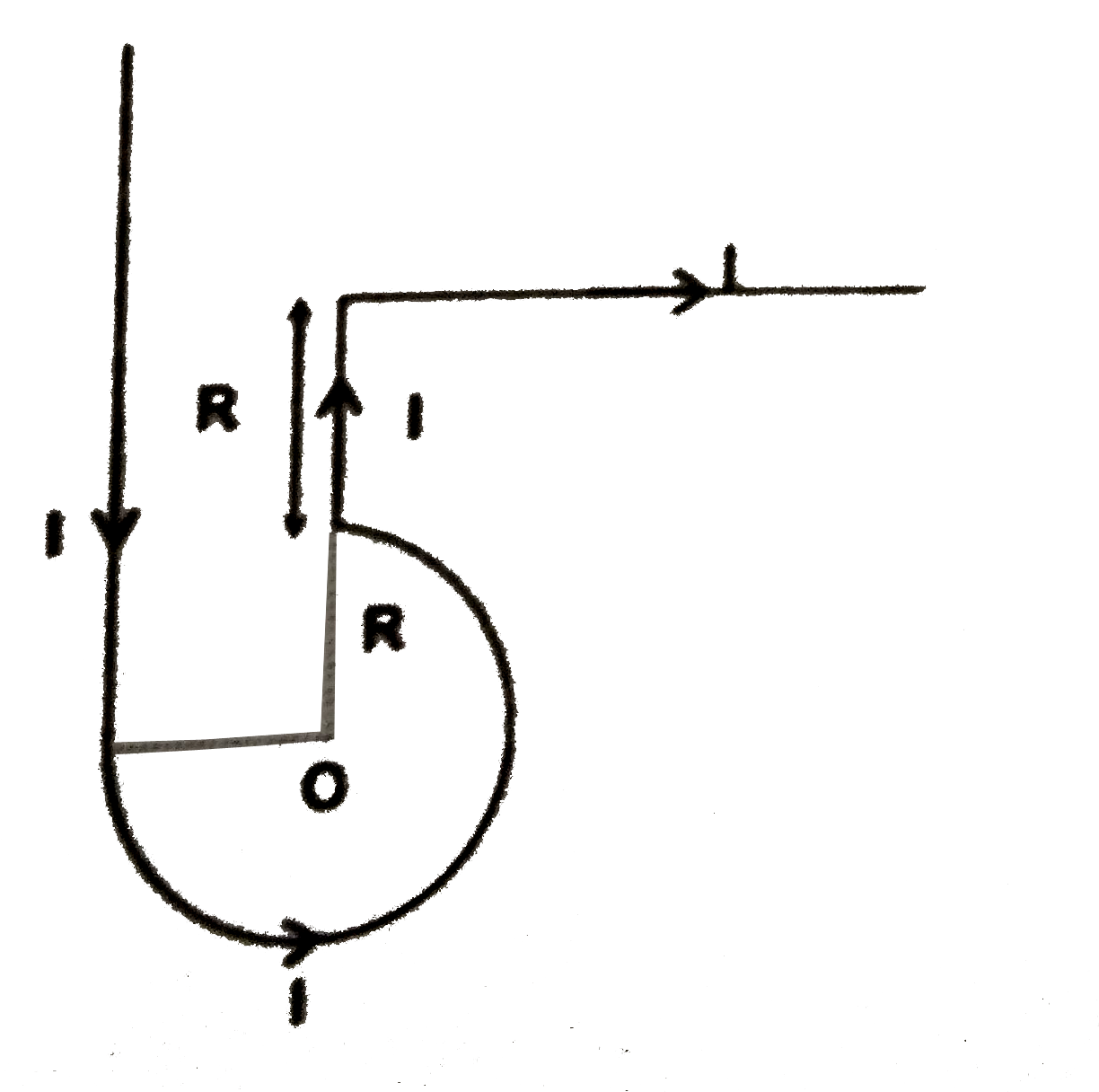
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)A circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
AπBr2t(1−π2)BπBr2t(1−π3)CπBr2t(1−π4)DπBr2t(1−π5)
An electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
View SolutionAn electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
View SolutionA wire carrying current i is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed
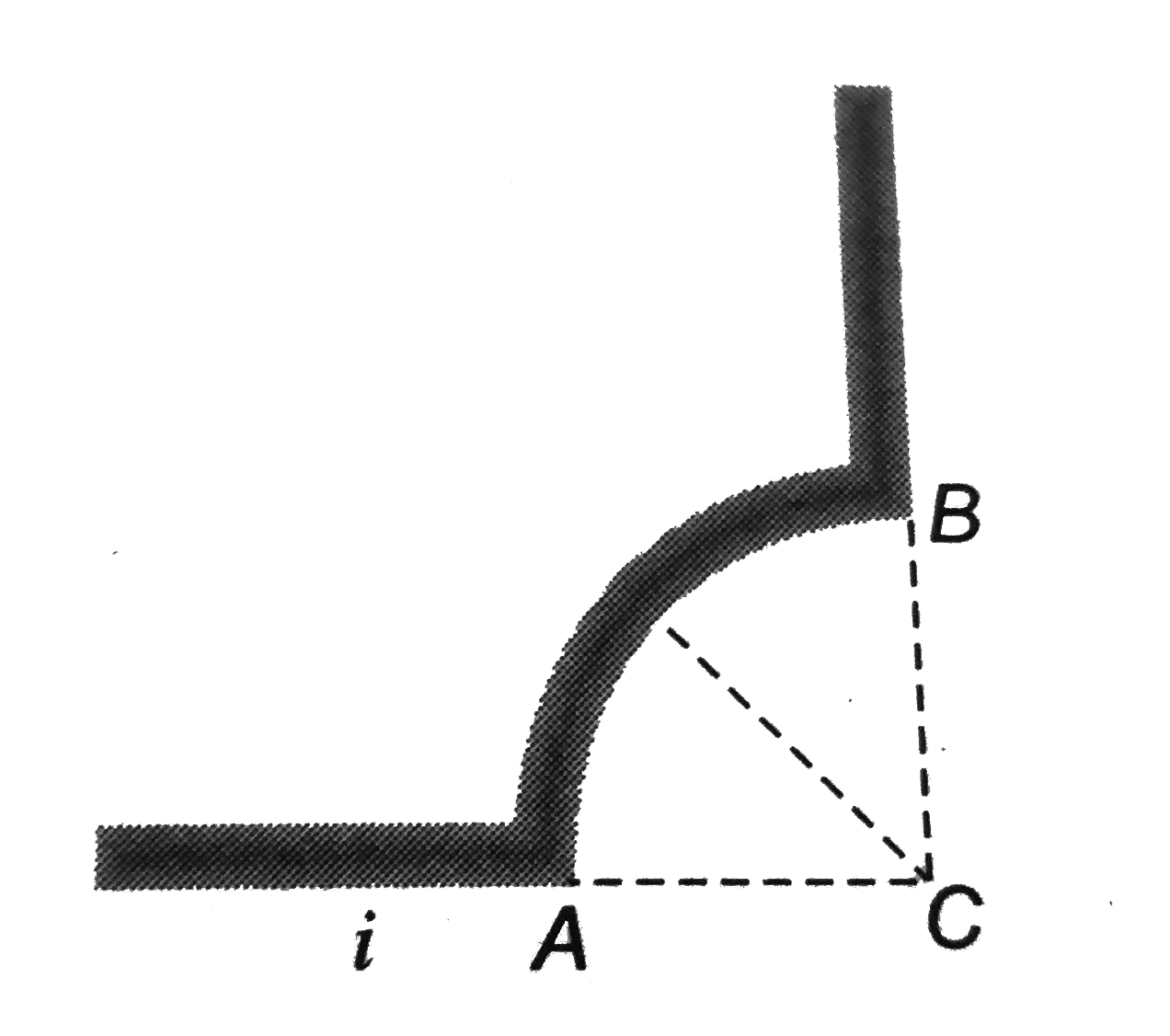
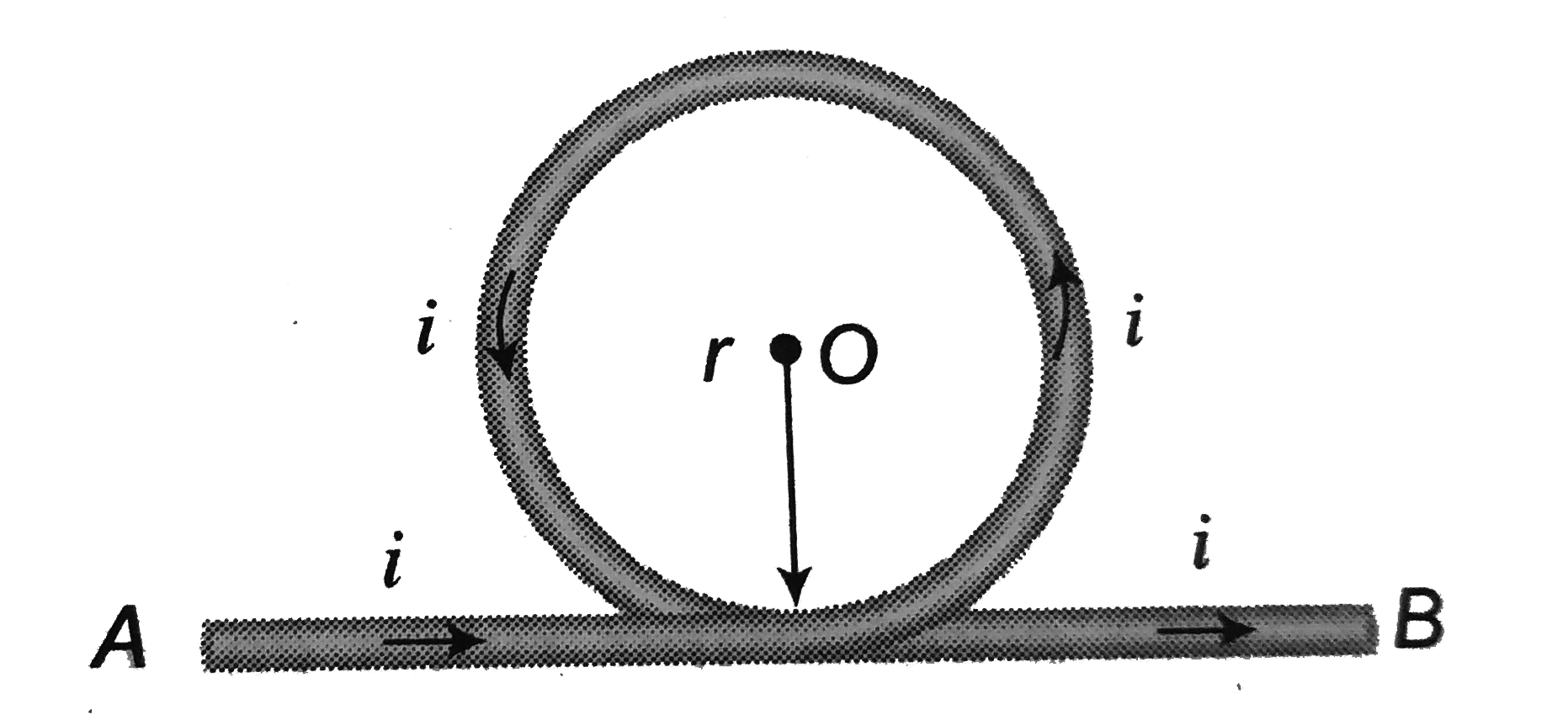
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
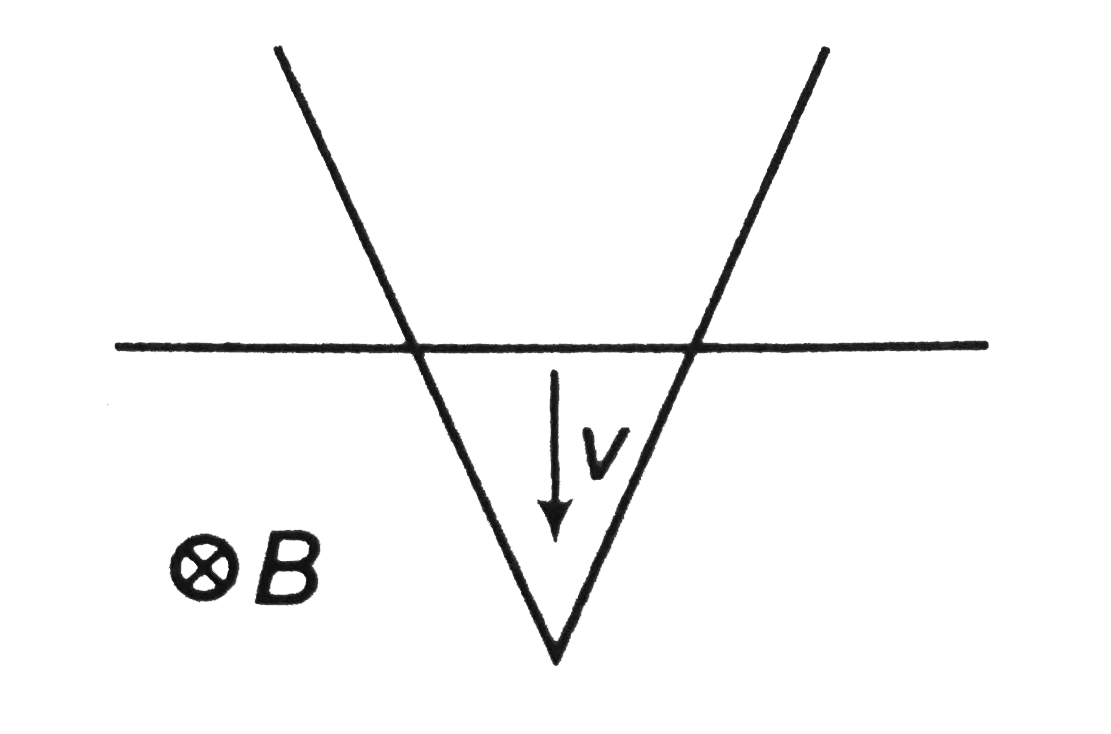
View SolutionA wire is bent in the form of a V shape and placed in a horizontal plane. There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
View Solution
