What is torsional constant of the spring used in a galvanometer?
To find the torsional constant of the spring used in a galvanometer, we need to understand the relationship between the torque acting on the loop in the magnetic field and the torsional constant of the spring. Here’s a step-by-step solution:
Step 1: Understanding Torque in a Magnetic Field
When a current-carrying loop is placed in a magnetic field, it experiences a torque. The torque (τ) on the loop can be expressed using the formula:
τ=m×B
where m is the magnetic moment of the loop, and B is the magnetic field.
Step 2: Defining Magnetic Moment
The magnetic moment (m) of the loop can be defined as:
m=I⋅A
where I is the current flowing through the loop and A is the area of the loop.
Step 3: Relating Torque to Deflection
As the loop experiences torque, it starts to rotate, leading to a deflection (θ). The torque due to the spring (restoring torque) can be expressed as:
τ=k⋅θ
where k is the torsional constant of the spring and θ is the angular deflection.
Step 4: Setting the Torques Equal
At equilibrium, the torque due to the magnetic field is equal to the restoring torque of the spring:
m⋅B=k⋅θ
Step 5: Solving for the Torsional Constant
Rearranging the equation gives us the expression for the torsional constant k:
k=m⋅Bθ
Conclusion
Thus, the torsional constant of the spring used in a galvanometer can be determined using the above relationship, where you need to know the magnetic moment, the magnetic field strength, and the deflection angle.
---
When a current-carrying loop is placed in a magnetic field, it experiences a torque. The torque (τ) on the loop can be expressed using the formula:
τ=m×B
where m is the magnetic moment of the loop, and B is the magnetic field.
The magnetic moment (m) of the loop can be defined as:
m=I⋅A
where I is the current flowing through the loop and A is the area of the loop.
As the loop experiences torque, it starts to rotate, leading to a deflection (θ). The torque due to the spring (restoring torque) can be expressed as:
τ=k⋅θ
where k is the torsional constant of the spring and θ is the angular deflection.
At equilibrium, the torque due to the magnetic field is equal to the restoring torque of the spring:
m⋅B=k⋅θ
Rearranging the equation gives us the expression for the torsional constant k:
k=m⋅Bθ
Thus, the torsional constant of the spring used in a galvanometer can be determined using the above relationship, where you need to know the magnetic moment, the magnetic field strength, and the deflection angle.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Revision Exercises (Additional Questions )
Explore 16 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Revision Exercises (Fill in the Blanks )
Explore 10 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Higher Order Thinking Skills & Advanced Level
Explore 10 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
Similar Questions
Knowledge Check
What will be the force constant of the spring system shown in figure?
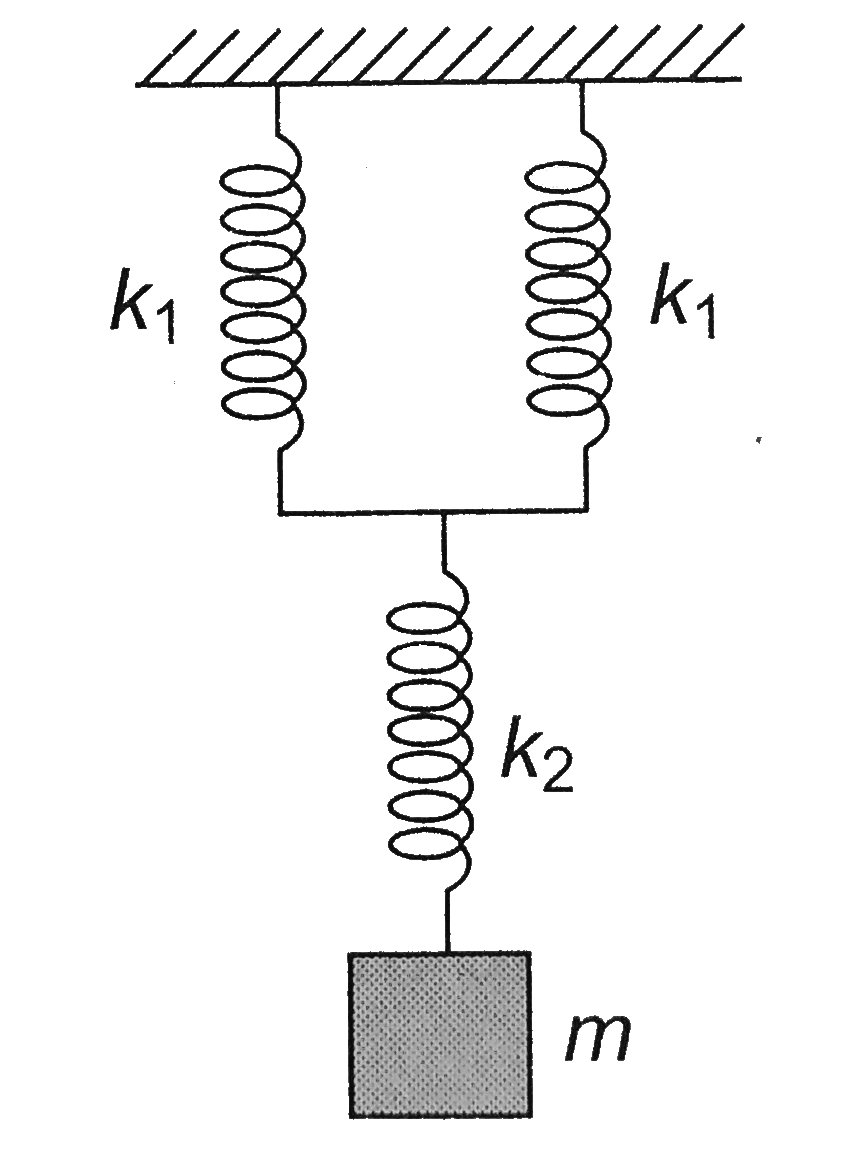 A[1k1+1k2]B[12k1+1k2]−1C[1k1+1k2]−1D[12k1+1k2]
A[1k1+1k2]B[12k1+1k2]−1C[1k1+1k2]−1D[12k1+1k2]
Define force constant of spring .
View SolutionFind the time period of the oscilltion of mass m in figure a and b. What is the equivalent spring constant of the spring in each case. ?

View SolutionIn a moving coil galvanometer, a rectangular coil of N turns, area of cross-section A and moment of inertia l is suspended in a radial field B through a spring.
(a) If a current i0 produces a deflection of π4 in the coil, find the torsional constant of the spring
(b) Find the maximum deflection surffered by the coil, if a charge Q is passed through it in a short interval of time
View SolutionTwo moving coil galvanometers A and B have rectangular coil of 100 turns each. The area of coil of galvanometers A and B are 2×10−4m2 and 6×10−4m2 respectively. Calculate the ratio of current sensitivity of A to B if coils in both salvanometers are kept in a radial horizontal magnetic field of 0.2 T and the torsional constant of hair springs are also same.
View SolutionWhat will be the equivalent spring constant of the spring system shown in the figure ?

View SolutionWhat are the advantagges of using soft iron as a core, instead of steel, in the coils of galvanometers?
View SolutionWhat will be the spring constant k of a. spring if length of the spring is made n times?
View Solution

