A long conducting wire is placed along Y-axis and a current of 5 A is flowing through it in positive Y-axis. A charged particle of charge +3.2×10−19 C is moving parallel to the conductor towards negative Y-axis with a speed of 5×104ms−1. Calculate the force exerted by the magnetic field of current on charged particle. The perpendicular distance between charged particle and wire is 25 cm.
The correct Answer is:6.4×10−20N towards + X - axis
To solve the problem, we need to calculate the magnetic force exerted on a charged particle moving in the magnetic field created by a long conducting wire carrying a current. Here are the steps to find the solution:
Step 1: Identify the Given Values
- Current (I) = 5 A (flowing in the positive Y-direction)
- Charge of the particle (q) = +3.2×10−19 C
- Speed of the charged particle (v) = 5×104 m/s (moving in the negative Y-direction)
- Perpendicular distance (d) from the wire = 25 cm = 0.25 m
Step 2: Calculate the Magnetic Field (B) due to the Wire
The magnetic field around a long straight conductor carrying current is given by the formula:
B=μ0I2πd
where μ0=4π×10−7T m/A.
Substituting the values:
B=(4π×10−7)×52π×0.25
B=(4×10−7)×50.5=4×10−6T
Step 3: Determine the Direction of the Magnetic Field
Using the right-hand rule, if the current is flowing in the positive Y-direction, the magnetic field will circulate around the wire. At the position of the charged particle (which is below the wire), the magnetic field will be directed in the negative Z-direction.
Step 4: Calculate the Force (F) on the Charged Particle
The magnetic force experienced by a charged particle moving in a magnetic field is given by:
F=q(v×B)
Since the charged particle is moving in the negative Y-direction and the magnetic field is in the negative Z-direction, we can use the right-hand rule to find the direction of the force.
1. The velocity vector →v=−v^j
2. The magnetic field vector →B=−B^k
Now, calculate the cross product:
v×B=(−v^j)×(−B^k)=vB(^j×^k)=vB^i
Step 5: Substitute the Values into the Force Equation
Now substituting the values:
F=q(vB)
Substituting B=4×10−6T:
F=(3.2×10−19)×(5×104)×(4×10−6)
Calculating:
F=(3.2×10−19)×(2×10−1)=6.4×10−20N
Step 6: Determine the Direction of the Force
The force is directed along the positive X-axis (as determined from the right-hand rule).
Final Answer
The force exerted by the magnetic field on the charged particle is:
F=6.4×10−20N(in the positive X-direction)
---
- Current (I) = 5 A (flowing in the positive Y-direction)
- Charge of the particle (q) = +3.2×10−19 C
- Speed of the charged particle (v) = 5×104 m/s (moving in the negative Y-direction)
- Perpendicular distance (d) from the wire = 25 cm = 0.25 m
The magnetic field around a long straight conductor carrying current is given by the formula:
B=μ0I2πd
where μ0=4π×10−7T m/A.
B=(4π×10−7)×52π×0.25
B=(4×10−7)×50.5=4×10−6T
Using the right-hand rule, if the current is flowing in the positive Y-direction, the magnetic field will circulate around the wire. At the position of the charged particle (which is below the wire), the magnetic field will be directed in the negative Z-direction.
The magnetic force experienced by a charged particle moving in a magnetic field is given by:
F=q(v×B)
Since the charged particle is moving in the negative Y-direction and the magnetic field is in the negative Z-direction, we can use the right-hand rule to find the direction of the force.
2. The magnetic field vector →B=−B^k
v×B=(−v^j)×(−B^k)=vB(^j×^k)=vB^i
Now substituting the values:
F=q(vB)
Substituting B=4×10−6T:
F=(3.2×10−19)×(5×104)×(4×10−6)
Calculating:
F=(3.2×10−19)×(2×10−1)=6.4×10−20N
The force is directed along the positive X-axis (as determined from the right-hand rule).
The force exerted by the magnetic field on the charged particle is:
F=6.4×10−20N(in the positive X-direction)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Conceptual Questions
Explore 29 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Tough & Tricky (PROBLEMS )
Explore 15 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:CHAPTER PRACTICE TEST
Explore 13 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
Similar Questions
A charged particle of charge 2⋅0μC moving along x-axis with a speed of 3×106ms−1 enters a magnetic field, →B=(0⋅3ˆj+0⋅4ˆk) tesla acting in a specific. What is the magnitude of magnetic force on the charged particle?
View SolutionMagnetic Force on Charge||Path of Charged Particle Moving Perpendicular to Magnetic Field||Charged Particle Moving Along Magnetic Field
View Solution
Knowledge Check
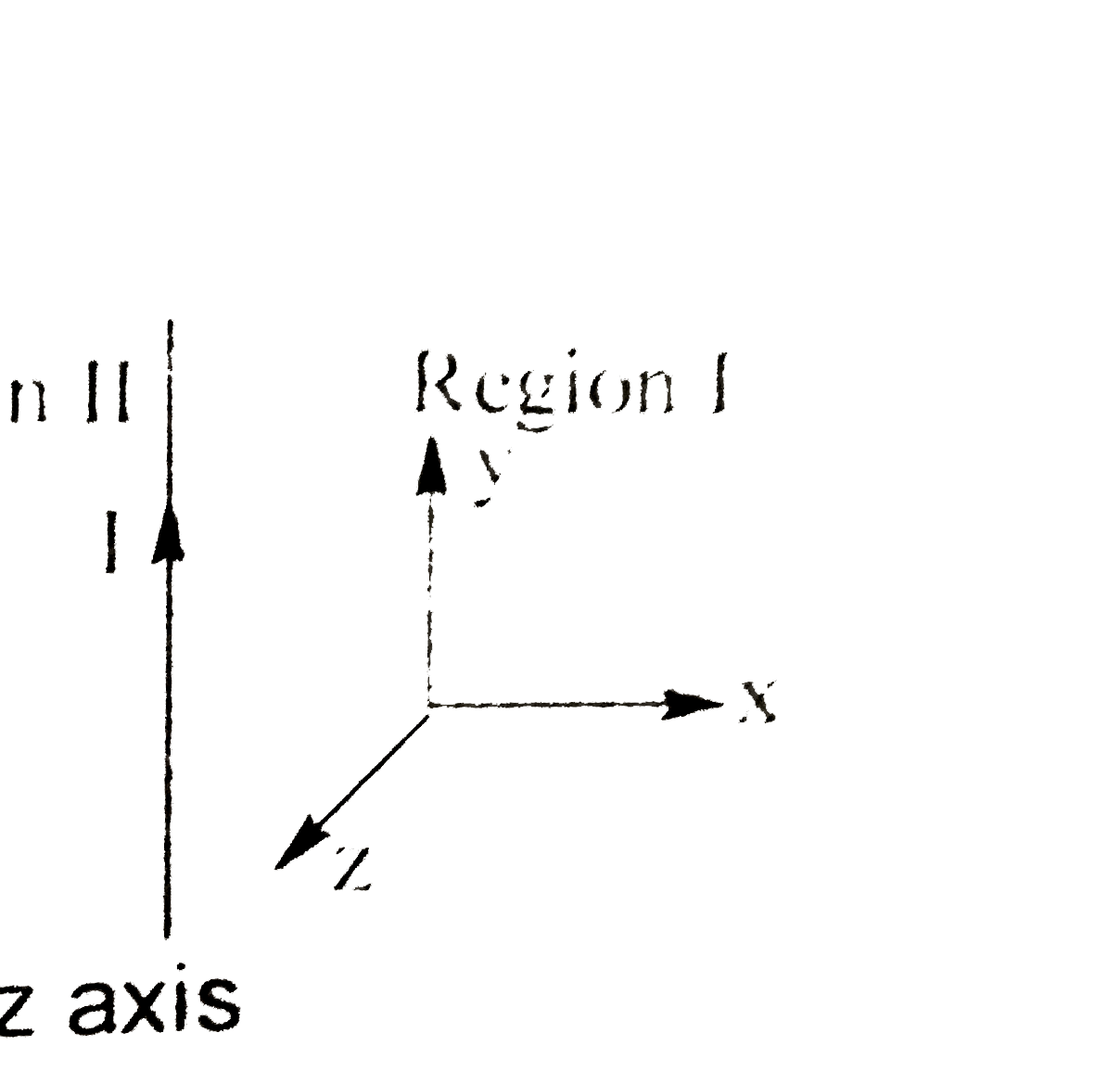
A inifinite length current carrying wire is placed in x,y plane parallel to y axis as shown in figure. (All charges projected in region l)AA positively charged particle projected along y axis will get deflected along z axisBA positively charged particle projected along x axis will get deflected along y axisCA negatively charged particle projected along x axis will get deflected along +y axisDA negatively charged particle projected along x axis will get deflected along +z axisThe magnetic force acting on a charged particle of charge −2μC in a magnetic field of 2T acting y direction, when the particle velocity is (2i+3ˆj)×106ms−1, is
A8N in −z directionB4N in z directionC8N in y directionD8N in z directionA charged particle is moved along a magnetic field line. The magnetic force on the particle is
Aalong its velocityBopposite to its velocityCperpendicular to its velocityDzero
In a region of magnetic field 0.05 T directed along positive direction of Y-axis, a beam of charged particles enters the region along X-axis with a velocity of 2.5×104ms−1. Calculate the radius of circular path described by the charge particles if their charge to mass ratio is 7.5×106Ckg−1.
View SolutionMagnetic Force on Charge||Path OF Charge Particle Moving Perpendicular to Magnetic Field||Charge Particle Moving Along Magnetic Field
View SolutionA charge of+2.0×10−8C is placed on the positive place and a charge of -1.0×10−8Conthe¬ativeplateofaparal≤l−plate∩aci→rof∩acitance 1.2 xx (10^-3) mu F. Calculate the potential difference developed between the plates.
View SolutionThere is one circular current carrying loop. A charged particle is projected with a certain speed along the axis of the coil. How will the coil exert magnetic force on the charged particle?
View SolutionA uniform magnetic field of 30 mT exists in the +X direction. A particle of charge +ve and mass 1.67×10−27 kg is projected through the field in the + y direction with a speed of 4.8×106 m/s
(a) find the force on the charged particle in magnitude and direction
(b) find the force if the particle were negatively charged.
(c ) Describe the nature of path followed by the particle in both the cases
View Solution