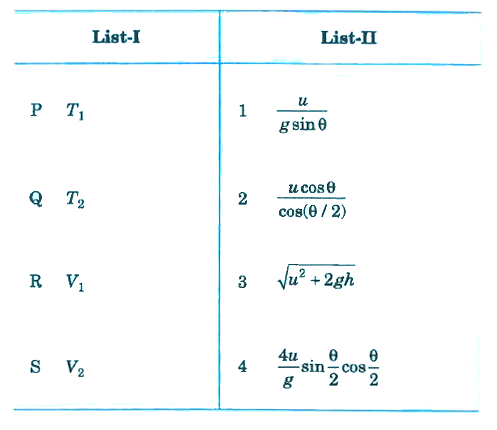
A particle is projected from the top of a tower of height h with a speed u at an angle $θ$ above the horizontal .
$T_{1}$ =Time taken by the projectile to reach the height of tower again .
$T_{2}$ =Time taken by the projectile to move at right angle to initial direction of motion .
$V_{1}$ =Speed of the projectile when it moves at an angle $θ / 2$ with the horizontal .
$V_{2}$ =Speed with projectile strikes the ground .
.

$\begin{matrix} P & Q & R & S 4 & 1 & 2 & 3 \end{matrix}$

$\begin{matrix} P & Q & R & S 1 & 2 & 3 & 4 \end{matrix}$

$\begin{matrix} P & Q & R & S 2 & 4 & 1 & 3 \end{matrix}$

$\begin{matrix} P & Q & R & S 2 & 1 & 3 & 4 \end{matrix}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A particle is projected from the top of a tower of height h with a speed u at an angle theta above the horizontal . T_(1)=Time taken by the projectile to reach the height of tower again . T_(2)=Time taken by the projectile to move at right angle to initial direction of motion . V_(1)=Speed of the projectile when it moves at an angle theta//2 with the horizontal . V_(2)=Speed with projectile strikes the ground . . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Knowledge Check

A projectile is projected with speed u at an angle $θ$ with the horizontal . The average velocity of the projectile between the instants it crosses the same level is
Au cos $θ$
Bu sin $θ$
Cu cot $θ$
Du tan $θ$
A projectile is fired with a velocity v at right angle to the slope inclined at an angle $θ$ with the horizontal. The range of the projectile along the inclined plane is

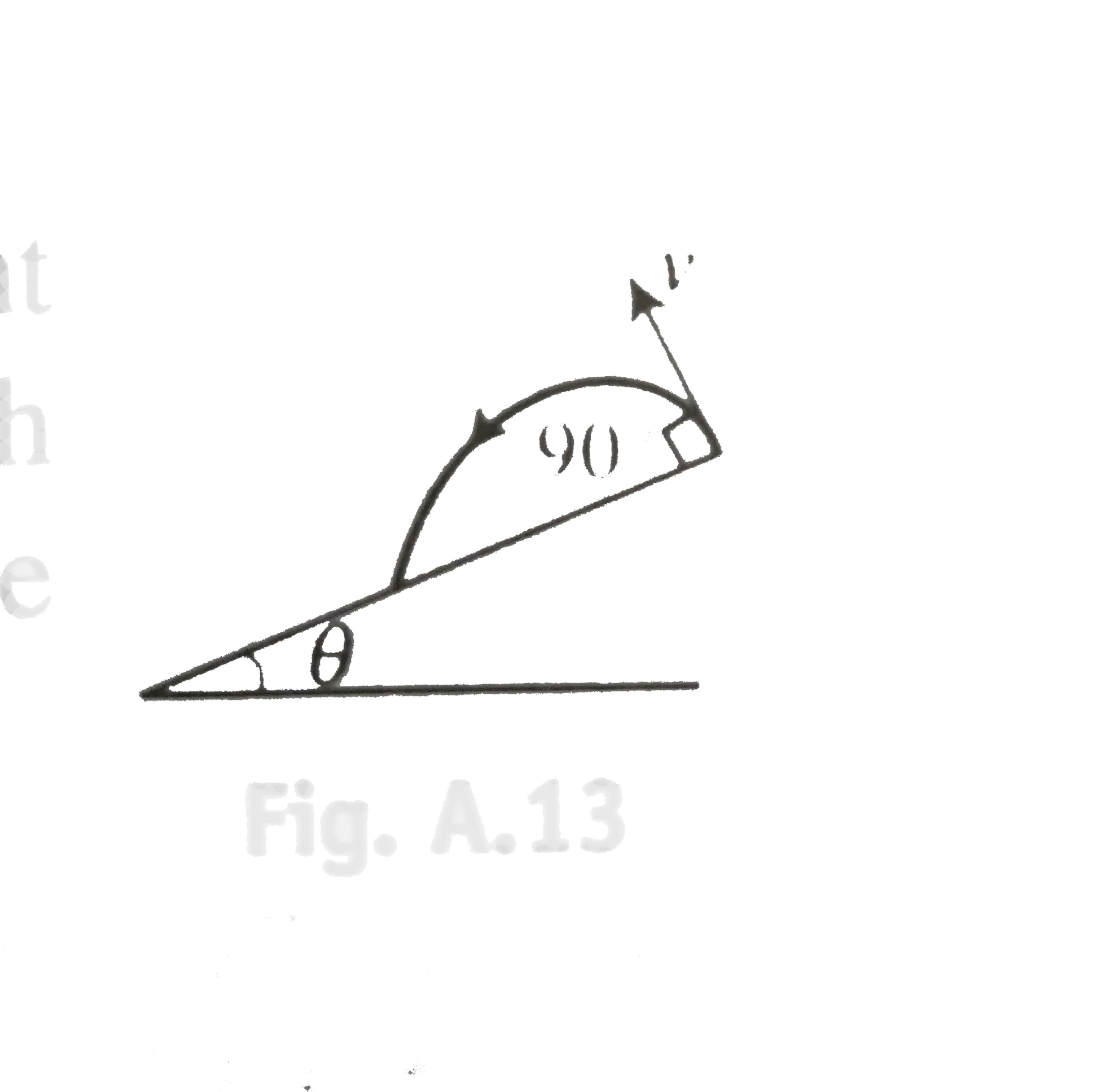A $\frac{2 v^{2} tan θ}{g}$
B $\frac{v^{2} sec θ}{g}$
C $\frac{2 v^{2} tan θ sec θ}{g}$
D $\frac{v^{2} sin θ}{g}$
A particle is projected in air with an initial velocity u directed at an angle $θ$ above horizontal. After time $t_{0}$ the velocity of the particle is directed at angle $ϕ$ above horizontal.
AAt time $t_{0}$ magnitude of verticle component of velocity of the particle is $u cos θ cot ϕ$
BAt time $t_{0}$ magnitude of rate of change of speed of the particle is $g sin ϕ$
CThe radius of curvature of the trajectory at time $t_{0}$ is $\frac{u^{2} {cos}^{2} θ}{g {cos}^{3} ϕ}$
DThe value of time $t_{0}$ is $u cos θ (tan θ - tan ϕ) / g$ .

MODERN PUBLICATION-MOTION IN A PLANE -COMPETITION FILE OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS)

Home
Ask Doubt
Profile

The correct Answer is:a

Topper's Solved these Questions

Similar Questions

Knowledge Check

A projectile is projected with speed u at an angle θ with the horizontal . The average velocity of the projectile between the instants it crosses the same level is

A projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

A particle is projected in air with an initial velocity u directed at an angle θ above horizontal. After time t0 the velocity of the particle is directed at angle ϕ above horizontal.

MODERN PUBLICATION-MOTION IN A PLANE -COMPETITION FILE OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS)

A projectile is projected with speed u at an angle $θ$ with the horizontal . The average velocity of the projectile between the instants it crosses the same level is

A projectile is fired with a velocity v at right angle to the slope inclined at an angle $θ$ with the horizontal. The range of the projectile along the inclined plane is

A particle is projected in air with an initial velocity u directed at an angle $θ$ above horizontal. After time $t_{0}$ the velocity of the particle is directed at angle $ϕ$ above horizontal.