Find the components of a vector →A=2ˆi+3ˆj along the directions of ˆi+ˆj and ˆi−ˆj
Video Solution
Text Solution
Magnitude of the vector ˆi+ˆj
∣∣∣→ˆi+ˆj∣∣∣=√(1)2+(1)2=√2
tanθ=∣∣ˆj∣∣∣∣ˆi∣∣=1
ˆi+ˆj makes an angle of 45∘ with direction of the X-axis .
Magnitude of the (ˆi−ˆj)
∣∣ˆi−ˆj∣∣=√12+(−1)2=√2
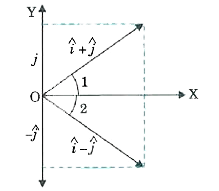
tanθ=−∣∣ˆj∣∣∣∣ˆi∣∣=−1
ˆi−ˆj makes an angle of −45∘ with direction of the X-axis.
To find the Component of vector →A=2ˆi+3ˆj alomg the direction (ˆi+ˆj)
Let →B=ˆi+ˆj
→A.→B=ABcosθ=(acosθ)B
∴Acosθ→A.→BB
=(2ˆi+3ˆj).(ˆi+ˆj)√(1)2+(1)2
=(2+3)√2=5√2⎡⎢⎣∴Acosθ=∣∣→A∣∣∣∣→B∣∣⎤⎥⎦
To find the component of vector →A=2ˆi+3ˆj along the direction (ˆi−ˆj)
Let →B=ˆi−ˆj
Similarly Acosθ=→A.→Bb
=(2ˆi+3ˆj).(ˆi−ˆj)√(1)2+(−1)2
(2−3)√2=−1√2
|
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) (NCERT (Additional Exercises))
7 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) (NCERT (Exemplar Problems Subjective Questions) Very short nswer type questions)
13 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - TOUGH & TRICKY PROBLEMS
14 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
Knowledge Check
The component of vector →A=2ˆi+3ˆj along the direction of (ˆi−ˆj) is
A1√2B−1√2C12D−12The component of vector A=2ˆi+3ˆj along the vector ˆi+ˆj is
A5√2B10√2C5√2D5The component of vector →A=axˆi+ayˆj+azˆk along th direction of (ˆi−ˆj) is
A(ax−ay+az)B(ax−ay)C(ax−ay√2D(ax+ay+az)
ˆi and ˆj are unit vectors along x-axis and y-axis respectively what is the magnitude and direction of the vector ˆi+ˆj and ˆi−ˆj ? What are the magnitudes of components of a vector →a=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj?
View SolutionFind the components of →a=2ˆi+3ˆj along the direction of vectors ˆi+ˆj and ˆi−ˆj.
View SolutionFind the vector components of →a=2ˆi+3ˆj along the directions of ˆi+ˆj.
View SolutionCalculate the component of vector →A=(6ˆi+5ˆj) along the directions of (ˆi−ˆj)and(ˆi+ˆj).
View SolutionFind he component of →a=2ˆi+3ˆj along the direction of vectors (ˆi+ˆj)
View Solution
