Obtain the equation for radius of illumination (or) Snell's window. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

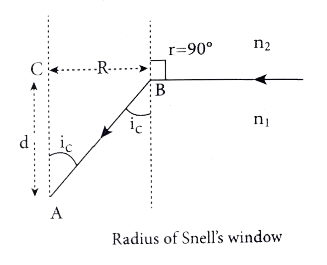
The radius of Snell’s window can be deduced with the illustration as shown in figure. Light is seen from a point A at a depth d. The Snell’s law in product form, equation $n_{2} sin i = n_{2} sin r$ for the refraction happening at the point B on the boundary between the two media is,
$n_{1} s i \in i_{c} = n_{2} {sin 90}^{\circ}$ ...(1)
$n_{1} {sin i}_{c} = n_{2} ∵ {sin 90}^{\circ} = 1$
${sin i}_{C} = \frac{n_{2}}{n_{1}}$ ...(2)
From the right angle triangle $Δ$ ABC,
${sin i}_{c} = \frac{C R}{A B} = \frac{R}{\sqrt{d^{2} + R^{2}}}$ ...(3)
Equating the above two equation (3) and equation (2),
$\frac{R}{\sqrt{d^{2} + R^{2}}} = \frac{n_{2}}{n_{1}}$
Squaring on both sides, $\frac{R^{2}}{R^{2} + d^{2}} = {(\frac{n_{2}}{n_{1}})}^{2}$
Taking reciprocal, $\frac{R^{2} + d^{2}}{R^{2}} = {(\frac{n_{1}}{n_{2}})}^{2}$
On further simplifying,
$1 + \frac{d^{2}}{R^{2}} = {(\frac{n_{1}}{n_{2}})}^{2}, \frac{d^{2}}{R^{2}} = {(\frac{n_{1}}{n_{2}})}^{2} - 1, \frac{d^{2}}{R^{2}} = \frac{n_{1}^{2}}{n_{2}^{2}} - 1 = \frac{n_{1}^{2} - n_{2}^{2}}{n_{2}^{2}}$
Again taking reciprocal and rearranging
$\frac{R^{2}}{d^{2}} = \frac{n_{2}^{2}}{n_{1}^{2} - n_{2}^{2}}, R^{2} = d^{2} = (\frac{n_{2}^{2}}{n_{1}^{2} - n_{2}^{2}})$
The radius of illumination is,
$R = d \sqrt{\frac{n_{2}^{2}}{n_{1}^{2} - n_{2}^{2}}}$ ...(4)
If the rarer medium outside is air, then, $n_{2}$ = 1, and we can take $n_{1}$ = n
$R = d (\frac{1}{\sqrt{n^{2} - 1}})$ (or) $R = \frac{d}{\sqrt{n^{2} - 1}}$ ...(5)

Updated on:21/07/2023

|

Class 12 PHYSICS SAMPLE PAPER -10 (SOLVED)

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER -10 (SOLVED)-PART - IV

Home
Ask Doubt
Profile