Question

Obtain a relation for the magnetic induction at a point along the axis of a circular coil carrying current.

Explanation

Magnetic field produced along the axis of the current carrying circular coil: Consider a current carrying circular loop of radius R and let I be the current flowing through the wire in the direction. The magnetic field at a point P on the axis of the circular coil at a distance z from its center of the coil O. It is computed by taking two diametrically opposite line elements of the coil each of length `vec(dl)` at C and D. Let `vecr` be the vector joining the current element `(Ivec(dl))` at C to the point P.
`PC=PD=r=sqrt(R^(2)+Z^(2))`and angle `/_CPO=DPO=theta`
According to Biot-Savart.s law, the magnetic field at P due to the current element `Ivec(dl)` is `dvecB=(mu_(0))/(4pi)(Ivec(dl)xxhatr)/(r^(2))`
The magnitude of magnetic field due to current element `Ivec(dl)` at C and D are equal because of equal distance from the coil. The magnetic field `dvecB` due to each current element I`vec(dl)` is resolved into two components, dB sin `theta` along y-direction and dB cos theta along z-direction Horizontal components of each current element cancels out while the vertical components `(dB cos thetahatk)` alone contribute to total magnetic field at the point P.

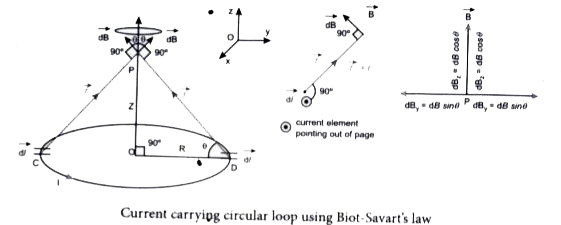
If we integrate `vecdl` around the loop, `dvecB` sweeps out a cone, then the net magnetic field `vecB` at point P is
`vecB=intdvecB=intdbcosthetahatk`
`vecB=(mu_(0)I)/(4pi)int(dl)/(r^(2))costhetahatk`
But cos `theta=(R)/((R^(2)+Z^(2))^(1/2))`
Using Pythagorous theorem `r^(2)=R^(2)+Z^(2)` and integrating line element from 0 to `2piR`, we get
`vecB=(mu_(0)I)/(4pi)=(R^(2))/((R^(2)+Z^(2))^(3/2))hatk`    ...(4)
Note that the magnetic field `vecB` points along the direction from the point O to P. Suppose if the current flows in clockwise direction, then magnetic field points in the direction from the point P to O.