Deduce the relation for the magnetic induction at a point due to an infinitely long straight conductor carrying current. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Magnetic field due to long straight conductor carrying current: Consider a long straight wire NM with current I flowing from N to M. Let P be the point at a distance a from point 0. Consider an element of length dl of the wire at a distance I from point O and $\to r$ be the vector joining the element dl with the point P. Let $θ$ be the.angle between dl and $\to r$ . Then, the magnetic field at P due to the element is
$d \to B = \frac{μ_{0} I d \to l}{4 π r^{2}} sin θ$ (Unit vector perpendicular to $\to d l$ and $\to r$ ) .........(i)
The direction of the field is perpendicular to the plane of the paper and going into it. This can be determined by taking the cross product between two vectors and $\to d l$ (let it be $ˆ n$ ). The net magnetic field can be determined by integrating equation with proper limits.
$\to B = \int d \to B$

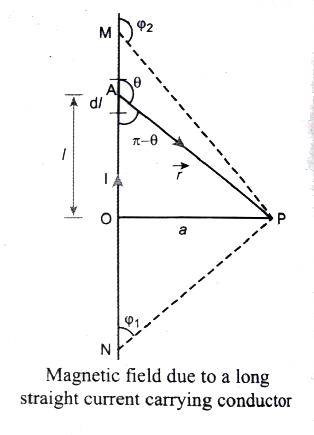
From the figure, in a right angle triangle PAO,
$tan (π - θ) = \frac{a}{l}$
$l = - \frac{a}{sin θ}$ ,since $tan (π - θ) = - tan θ \Rightarrow \frac{1}{tan θ} = cot θ$
$l = - a cot θ$ and $r = a cosec θ$
Differentiating,
$d l = a {cosec}^{2} θ, d θ$
$d \to B = \frac{μ_{0} I}{4 π} \frac{a {cosec}^{2} θ d θ}{{(a cosec θ)}^{2}} sin d θ ˆ$
$d \to B = \frac{μ_{0} I}{4 π a} sin θ d θ ˆ n$
This is the magnetic field at a point P due to the current in small elemental length. Note that we have expressed the magnetic field OP in terms of angular coordinate i.e. 0. Therefore, the net magnetic field at the point P which can be obtained by integrating $d \to B$ by varying angle from $θ = φ_{1}$ to $θ = φ_{2}$ is
$\to B = \frac{μ_{0} I}{4 π a} \int_{φ_{1}}^{φ_{2}} sin θ d θ ˆ n = \frac{μ_{0} I}{4 π a} ({cos φ}_{1} - {cos φ}_{2}) ˆ n$
Note that here $ˆ n$ represents the unit vector from the point O to P.

Updated on:21/07/2023

|

Class 12 PHYSICS SAMPLE PAPER 3 (SOLVED)

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER 3 (SOLVED)-PART- IV

Home
Ask Doubt
Profile