Derive the equation for acceptance angle and numerical aperture, of optical fiber. Acceptance angle in optical fibre:Solution in Tamil

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

To ensure the critical angle incidence in the core-cladding boundary inside the optical fibre, the light should be incident at a certain angle at the end of the optical fiber while entering in to it. This angle is called acceptance angle. It depends on the refractive indices of the cladding n 2 and the outer medium n 3 . Assume the light is incident at an angle called acceptance angle i a at the outer medium and core boundary at A.
The Snell.s law in the product form, equation for this refraction at the point A.
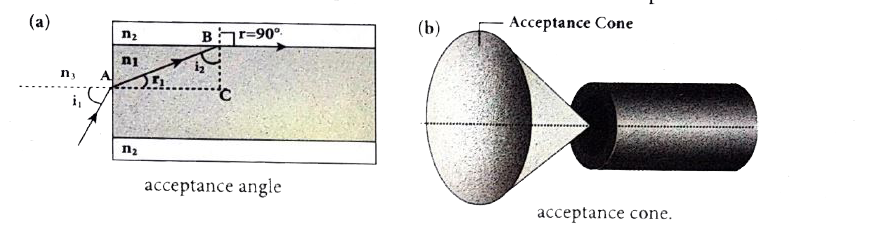
ocr_image
n 3 sin i a = n 1 sin r a
To have the total internal reflection inside optical fibre, the angle of incidence at the core-cladding interface at B should be atleast critical angle i c . Snell.s law in the product form,equation for the refraction at point b is
n 1 sin i c = n 2 sin 90 ∘
n 1 sin i c = n 2 sin 90 ∘ = 1
sin i c = n 2 n 1
From the right angle △ A B C ,
i c = 90 ∘ - r a
Now, equation (3) becomes, sin ( 90 ∘ - r a ) = n 2 n 1
Using trigonometry, cos r a = n 2 n 1
Substituting for cos r a
sin r a = 1 - ( n 2 ( n 1 ) 2 ) = n 1 2 - n 2 2 n 1 2 ... ... ... . ( 5 )
Substituting this in equation (1)
n 3 sin i a = n 1 n 1 2 - n 2 2 n 1 2 = n 1 2 - n 2 2 ... ... . ( 6 )
On further simplification,
sin i a = n 1 2 - n 2 2 n 3 ( or ) sin i a = n 1 2 - n 2 2 n 3 2 ... ... ... ( 7 )
i a = sin - 1 ( n 1 2 - n 2 2 n 3 2 ... ... ... ( 8 )
If outer medium is air, then n 3 = 1 . The acceptance angle i a becomes.
i a = sin - 1 ( n 1 2 - n 2 2 ...........(9)
Light can have any angle of incidence from 0 to i a with the normal at the end of the optical fibre forming a conical shape called acceptance cone. In the equation (6), the term ( n 3 sin i a ) is called numerical aperture NA of the optical fibre.
N A = n 3 sin i a ( n 1 2 - n 2 2 ... . . ( 10 )
If outer medium is air, then n 3 = 1 . The numberical aperture NA becomes,
N A = sin i a = n 1 2 - n 2 2 ... ... . ( 11 )

Updated on:21/07/2023
|
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions