Question

Explain the equivalent resistance of a series and parallel resistor network.

Explanation

Resistor in series: When two or more resistors are connected end to end, they are said to be in series. The resistors could be simple resistors or bulbs or heating elements or other devices. Fig. (a) shows three resistors `R_(1), R_(2) and R_(3)` connected in series.
The amount of charge passing through resistor `R_(2)` must also pass through resistors `R_(2) and R_(3)` since the charges cannot accumulate anywhere in the circuit. Due to this reason, the current I passing through all the three resistors is the same. According to Ohm.s law, if same current pass through different resistors of different values, then the potential difference across each resistor must be different. Let `V_(1), V_(2) and V_(3)` be the potential difference (voltage) across each of the resistors `R_(1),R_(2) and R_(3)` respectively, then we can write `V_(1)=IR_(1), V_(2)=IR_(2) and V_(3)=IR_(3)`. But the total voltage V is equal to the sum of voltages across each resistor.
`V=V_(1)+V_(2)+V_(3)`
`=IR_(1)+IR_(2)+IR_(3)" " ...(1)`
`V=I(R_(1)+R_(2)+R_(3))`
`V+I.R_(s)" "...(2)`
where `R_(s)` is the equivalent resistance,
`R_(s)=R_(1)+R_(2)+R_(3)" " ...(3)`
When several resistances are connected in series, the total or equivalent resistance is the sum of the individual resistances as shown in fig.(b).
Note: The value of equivalent resistance in series connection will be greater than each individual resistance.

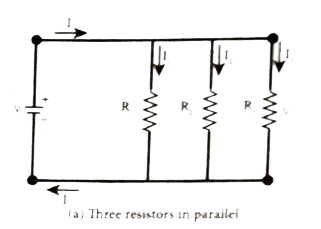
Resistors in parallel: Resistors are in parallel when they are connected across the same potential difference as shown in fig. (a).
In this case, the total current I that leaves the battery in split into three separate paths. Let `I_(1), I_(2) and I_(3)` be the current through the resistors `R_(1), R_(2) and R_(3)` respectively. Due to the conservation of charge, total current in the circuit I is equal to sum of the currents through each of the three resistors.
`I=I_(1)+I_(2)+I_(3)" "...(1)`
Since the voltage across each resistor is the same, applying Ohm.s law to each resistor, we have
`I_(1)=(V)/(R_(1)), I_(2)=(V)/(R_(2)), I_(3)=(V)/(R_(3))" " ...(2)`
Substituting these values in equation (1), we get
`I=(V)/(R_(1))+(V)/(R_(2))+(V)/(R_(3))=V[(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))]`
`I=(V)/(R_(p))`
`(1)/(R_(p))=(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3)) " " ...(3)`

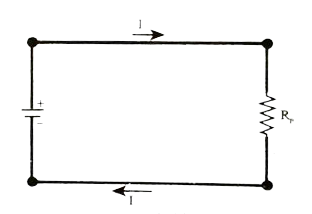
Here `R_(p)` is the equivalent resistance of the parallel combination of the resistors. Thus, when a number of resistors are connected in parallel, the sum of the reciprocal of the values of resistance of the individual resistor is equal to the reciprocal of the effective resistance of the combination as shown in the fig. (b).
Note: The value of equivalent resistance in parallel connection will be lesser than each individual resistance.