Explain the motion of blocks connected by a string in (i) vertical motion (ii) horizontal motion . Solution in Tamil

Video Solution

Text Solution

Verified by Experts

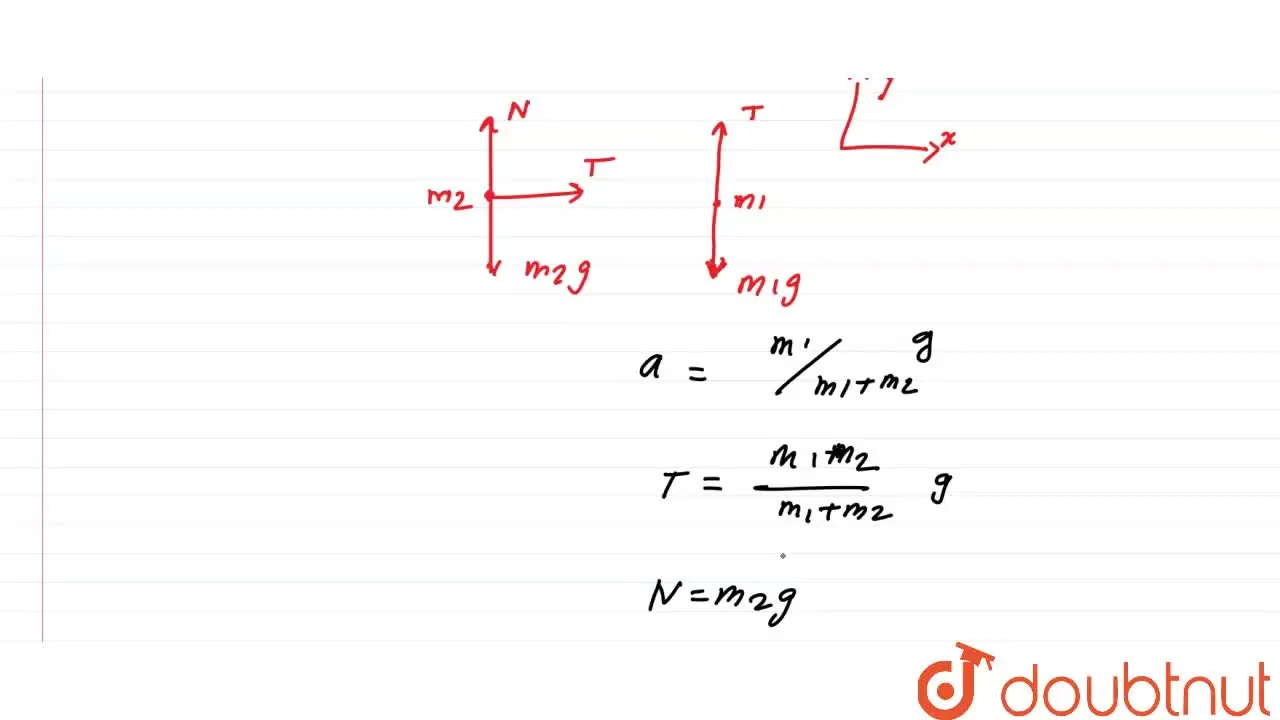
Vertical motion: Consider two blocks of masses $m_{1}$ and $m_{2} (m_{2} > m_{1})$ connected by a light and inextensible string that passes over a pulley as shown in Figure. Let the tension in the string be T and acceleration a. When the system is released, both the blocks start moving, $m_{2}$ vertically upward and $m_{1}$ downward with same acceleration a. The gravitational force $m_{1} g$ on mass $m_{1}$ is used in lifting the mass $m_{2}$
The upward direction is chosen as y direction. The free body diagrams of both masses are shown in Figure.

Applying Newton.s second law for mass $m_{2}$
$T ˆ j - m_{2} g ˆ j = m_{2} a ˆ j$
The left hand side of the above equation is the total force that acts on $m_{2}$ and the right hand side is the product of mass and acceleration of $m_{2}$ in y direction. By comparing the components on both sides, we get
$T - m_{2} g = m_{2} a$
Similarly, applying Newton.s second law for mass $m_{1}$
$T ˆ j - m_{1} g ˆ j = - m_{1} a ˆ j$
As mass $m_{1}$ moves downward ( $- ˆ j$ ), its acceleration is along ( $- ˆ j$ )
By comparing the components on both sides, we get
$T - m_{1} g = - m_{1} a$
$m_{1} g - T = m_{1} a$
Adding equations (1) and (2), we get
$m_{1} g - m_{2} g = m_{1} a + m_{2} a$
$(m_{1} - m_{2}) g = (m_{1} + m_{2}) a$
From equation (3), the acceleration of both the masses is
$a = (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g$
If both the masses are equal ( $m_{1} = m_{2}$ ), from equation (4)
a=0
This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest. To find the tension acting on the string, substitute the acceleration from the equation (4) into the equation (1).
$T - m_{2} g = m_{2} (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g$
$T = m_{2} g + m_{2} (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g$
By taking m,g common in the RHS of equation (5)
$T = m_{2} g (1 + \frac{m_{1} - m_{2}}{m_{1} + m_{2}})$
$T = m_{2} g (\frac{m_{1} + m_{2} + m_{1} - m_{2}}{m_{1} + m_{2}})$
$T = \frac{2 m_{1} m_{2}}{m_{1} + m_{2}} g$
Equation (4) gives only magnitude of acceleration.
For mass $m_{1}$ the acceleration vector is given by $\to a = - (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g ˆ j$
For mass m, the acceleration vector is given by $\to a = - (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g ˆ j$

Updated on:21/07/2023

|

Class 11 PHYSICS EXAMINATION QUESTION PAPER - JUNE 2019

Topper's Solved these Questions

Similar Questions

FULL MARKS-EXAMINATION QUESTION PAPER - JUNE 2019-PART IV

Home
Ask Doubt
Profile