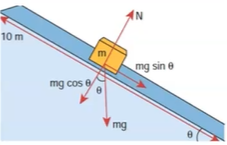
An object of mass m=1kg is sliding from top to bottom in the frictionless inclined plane of inclination angle θ=30∘ and the length of inclined plane is 10m as shown in the figure. Calculate the work done by gravitational force and normal force on the object Assume acceleration due to gravity, g=10ms−2
 Solution in Tamil
Solution in Tamil
We calculated in the previous chapter that the acceleration experienced by the object in the inclined plane as gsinθ
According to Newton.s second law, the force acting on the mass along the inclined plane F=mgsinθ . Note that this force is constant throughout the motion of the mass The work done by the parallel component of gravitational force (mgsinθ) is given by w=→F.d→r=Fdrcosϕ
where is the angle between the force (mgsinθ) and the direction of motion (d→r). In this case, force (mgsinθ) and the displacement (d→r) are in the same direction. Hence and cosϕ=1
wFdr=(mgsinθ)(dr) (dr=lenght of the inclined plane)
w=1×10×sin(30∘)×10=100×12=50J The component ing cos 6 and the normal force N are perpendicular to the direction of motion of the object, so they do not perform any work.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - FULL MARKSCHAPTER - WORK, ENERGY AND POWEREXERCISE - Textual Questions Solved (I. Multiple Choice Question:)
15 Videos
- WORK, ENERGY AND POWERBOOK - FULL MARKSCHAPTER - WORK, ENERGY AND POWEREXERCISE - Textual Questions Solved (II. Short Answer Questions)
5 Videos
- WAVES BOOK - FULL MARKSCHAPTER - WAVES EXERCISE - Additional Questions Solved (Numerical Problems )
10 Videos
Similar Questions
A uniform force of (2ˆi+ˆj) N acts on a particle of mass 1 kg. The particle displaces from position (3ˆj+ˆk) m to (5ˆi+3ˆj) m. The work done by the force on the particle is
View SolutionExplain how the definition of work in physics is different from general perception.
View SolutionThe fundamental frequency of a closed organ pipe is equal to the first overtone of an open organ pipe. If the length of the open pipe is 60 cm, What is the length of the closed pipe?
View SolutionA wooden box of mass 8kg slides down an inclined plane of inclination 30^(@) to the horizontal with a constant acceleration of 0.4ms^(-2) What is the force of friction between the box and inclined plane ? (g = 10m//s^(2)) .
View SolutionA body is allowed to slide from the top along a smooth inclined plane of length 5m at an angle of inclination 30^(@) .If g=10ms^(-2) , time taken by the body to reach the bottom of the plane is
View SolutionA block mass 'm' is placed on a frictionless inclined plane of inclination theta with horizontal. The inclined plane is accelerated horizontally so that the block does not slide down. In this situation vertical force exerted by the inclined plane on the block is:
View SolutionA block of mass l O kg is kept at the top of a rough inclined plane ofi_nclination 60° with the horizontal. The length of the inclined plane is 5 m and the coefficient of sliding friction between the block and the surface is 0.3. What is the work done on the block against the force of friction , when it reaches the bottom? (g =10m//s^2 )
View SolutionA mass of 1 kg is just able to slide down the slope of a rough inclined surface when the angle of inclination is 60°. What is the minimum force necessary to pull the mass up the inclined plane? (g =10m//s^2 )
View Solution300 J of work is done in sliding a 2 kg block up on inclined plane of height 10m. Work done against frictin is ( g=10ms^(-2) )
View SolutionThe mass of an object placed on an inclined plane is 2 kg and the angle of the inclined plane is 60 degrees, then the normal reaction force will be
View SolutionA body is allowed to slide from the top along a smooth inclined plane of length 5m at an angle of inclination 30°. If g=10ms2, time taken by the body to reach the bottom of the plane is
View SolutionA block of mass 5.0 kg slides down an incline of inclination 300 and length 10 m. find the work done by the force of gravity.
View SolutionThe length of a smooth inclined plane of inclination 30^(@) is 5m. The work done in moving a 10 kg mass from the bottom of the inclined plane to top is
View SolutionAn object of mass m is moved up a smooth inclined plane of inclination theta through a length l of the inclined plane and height h. What is the work done ?
View SolutionThe length of a smooth inclined plane of incilination 30^(@) is 5 m. The work done is moving a 10kg mass from the bottom of the inclined plane to top is
View Solution
