If either vector →a=→0 or →b=→0, then →a.→b=0.But the converse need not be true Justify your answer with an example.Solution in Tamil
The correct Answer is:Thus two non - zero vectors →a and →b may have →a.→b zero.
Step by step video, text & image solution for If either vector vec a = vec 0 or vec b = vec 0, then veca.vec b = 0.But the converse need not be true Justify your answer with an example. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.412videos
VECTOR ALGEBRA
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.12videos
VECTOR ALGEBRA
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.219videos
VECTOR ALGEBRA
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS134videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Find ∣∣→a×→b∣∣ if →a=ˆi−7ˆj+7ˆk and →b=3ˆi−2ˆj+2ˆk.
02:10View SolutionIn the figure which vectors are
(i) equal (ii) collinear (iii) coinitial
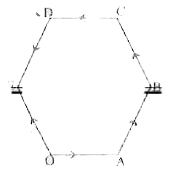 02:23View Solution
02:23View SolutionCompute the magnitude of the following vectors.
→a=ˆi+ˆj+ˆk, →b=2ˆi−7ˆj−3ˆk02:55View SolutionIf A+B+C=90∘ then
cotA+cotB+cotCcotAcotBcotC =04:19View SolutionIf either →a=0and →b=0then →a×→b=0. Is Is the converse true? Justify your answer with an example.
03:58View SolutionIf either →a=→0or →b=→0, then →a⋅→b=0 But the converse need not be true. Justify your answer with an example.
03:55View SolutionIf either →a=→0 or →b=→0 then →a.→b=→0 but, the converse need not be true. Justify your answer with an example.
01:49View Solutionयदि →a=0 अथवा →b=0 तब →a×→b=→0 होता है | क्या विलोम सत्य है ? उदाहरण सहित अपने उत्तर की पुष्टि कीजिए |
05:02View SolutionIf →a=→0or→b=→0 then →a.→b=0, show by an example that the converse of this statement is not always true .
04:34View Solutionसिद्ध करें की सदिश |→a|→b+∣∣→b∣∣→a और सदिश |→a|→b−∣∣→b∣∣→a एक-दूसरे पर लंब हैं, जहाँ →a≠→0,→b≠→0
02:34View SolutionIf →a=→b+→c, then is it true that |→a|=∣∣→b∣∣+|→c| ? Justify your answer.
04:20View SolutionIf either →a=→0 or →a×→b=→0 .Is the converse true? Justify your answer with an example.
03:25View SolutionIf either →a=0and →b=0then →a×→b=0. Is Is the converse true? Justify your answer with an example.
04:00View SolutionIf either →a=→0 or →b=→0 then →a.→b=→0 but, the converse need not be true. Justify your answer with an example.
02:24View SolutionIf either →a=→0 and →b=→0 then →a×→b=→0 . Is Is the converse true? Justify your answer with an example.
04:47View Solution
