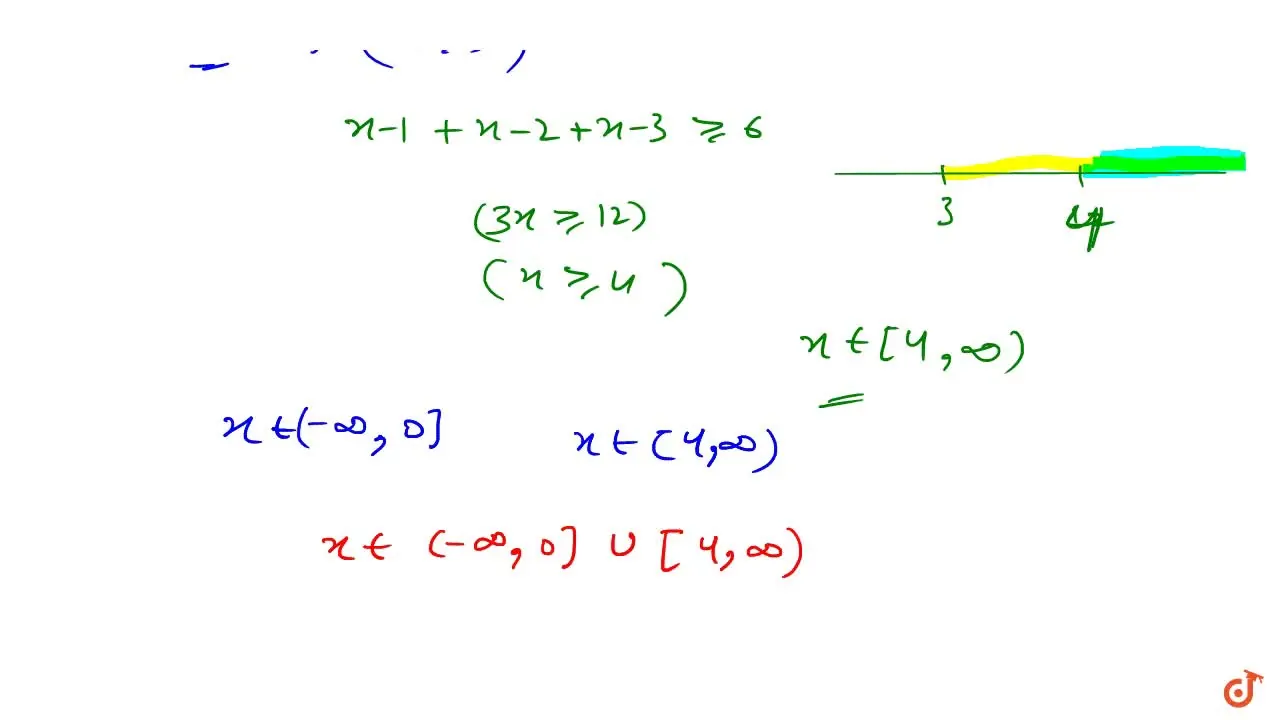|x−1|+|x−2|+|x−3|≥6
Video Solution
|
Answer
Step by step video & image solution for |x-1|+|x-2|+|x-3|geq6 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
Similar Questions
|x−1|+|x−2|+|x−3|≥6
View Solution|x−1|+|x−2|+|x−3|≥6
View SolutionIf x satisfies |x−1|+|x−2|+|x−3|≥6
View Solution|x−1|+|x−2|+|x−3|≥6, then
View SolutionFind the domain of f′(x) if f(x)=[x1+|x|]if |x|≥1,x1−|x|if |x|<1 fig
View SolutionLet f(x)={1|x|for|x|≥1ax2+bfor|x|<1⇔(x) is continuous and differentiable at any point, then a=12,b=−32 (b) a=−12,b=32 a=1,b=−1 (d) none of these
View SolutionFind the value of cos(sec−1x+c o s e c−1x) , |x|≥1
View SolutionSolve minz=x+y when the constraints are
x−y≥1
x−y≥0
x≥0
y≥0View Solution9x2−6x+1÷(3x−1)
View SolutionSolve the following linear programming problem: Minimize z=x+2y subject to 2x+y≥3,x+2y≥6,x,y≥0
View Solution