The sum of the interior angle of a 10-sided polygon is _______
1260∘
1440∘
1800∘
1620∘
The correct Answer is:B
The sum of interior angles of an n-sided polygon =(n−2)180∘.
∴ The sum of interior angles of a 10- sided polygon =(10−2)=180∘=1440∘
Hence, the correct option is (a).
Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level-3
Explore 19 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Test-1
Explore 12 Videos
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:Level-1
Explore 24 Videos
- FORMULASBook:PEARSON IIT JEE FOUNDATIONChapter:FORMULASExercise:ASSESSMENT TESTS (Test 2)
Explore 8 Videos
- INDICES Book:PEARSON IIT JEE FOUNDATIONChapter:INDICES Exercise:Test -2
Explore 12 Videos
Similar Questions
Knowledge Check
The sum of the interior angle of a 10-sided polygon is _______
A1260∘B1440∘C1800∘D1620∘The sum of the interior angles of a 12 sided regular polygon is equal to:
A180∘B360∘C1800∘D2160∘The sum of all the interior angles of a regular polygon is four times the sum of its exterior angles. The polygon is :
AhexagonBtriangleCdecagonDnonagon
The sum of interior angles of a polygon of n sides is __________right angles.
View SolutionWe know that the sum of the interior angles of a triangle is1800 . Show that the sums of the interior angles of polygons with 3,4,5,6 sides form an arithmetic progression. Find the sum of the interior angles of a 21 sided polygon.
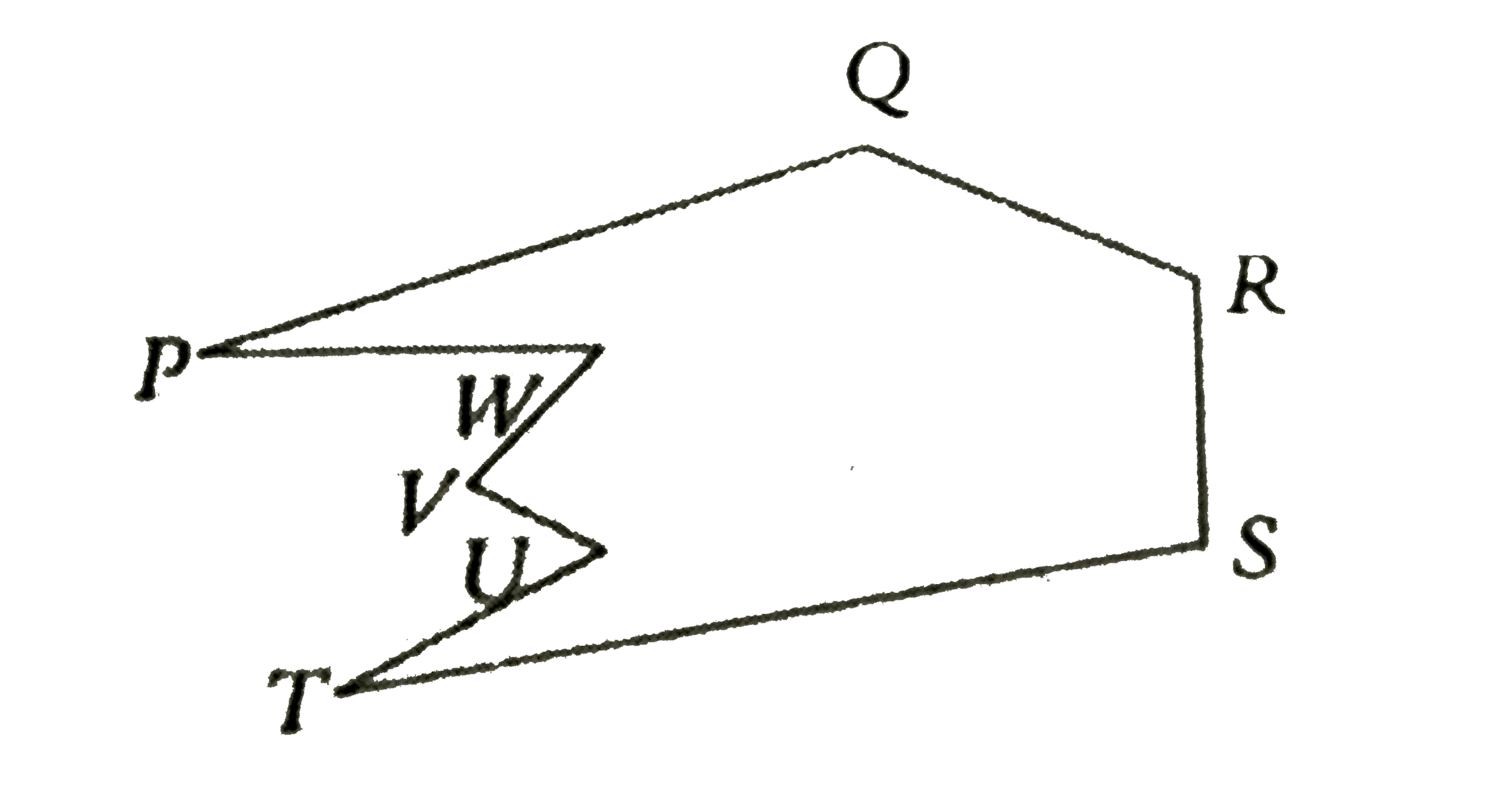
View SolutionFind the sum of the interior angles of the polygon gives below.
View SolutionConsider the following statements :
1. If n≥3 and m≥3 are distinct positive integers, then the sum of the exterior angles of a regular polygon of m sides is different from the sum of the exterior angles of a regular polygon of n sides.
2. Let m, n be integers such that m>n≥3. Then the sum of the interior angles of a regular polygon of m sides is greater than the sum of the interior angles of a regular polygon of n sides, and their sum is (m+n)π2.
Which of the above statements is/are correct?
View SolutionThe sum of all the interior angles of a regular polygon is four times the sum of its exterior angles. The polygon is :
View Solution
