In the figure above, ∠SPT=60∘and PQ=PR. Find ∠PQR
A
50∘
B
45∘
C
60∘
D
55∘
Video Solution
Text Solution
The correct Answer is:C
PQ=PR⇒∠PQR=∠PRQ
∠SPT=∠QPR
( ∵ vertically opposite angles are equal. )
∴∠QPR=60∘
∠PQR=∠PRQ=180−∠QPR2=60∘
Hence, the correct option is (c )
|
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-2
26 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-3
19 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Easy Type Question
15 Videos
- FORMULASBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
Similar Questions
Knowledge Check

In the figure above, ∠SPT=60∘and PQ=PR. Find ∠PQRA50∘B45∘C60∘D55∘
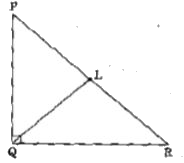
In the figure given above, ∠PQR=90∘ and QL is a median, PQ=5cmandQR=12cm, Then QL is equal to:
View Solution
In the figure, PQ=QR,∠RPQ=60∘,and∠QRS=20∘. Find the measure of ∠QSR.
View SolutionIn the given figure, ∠QPR=50∘,∠QRS=135∘ and PQ = PR and ST = SR. Find the angle of ∠S.

View SolutionIn the given figure if PQ||ST ,∠PQR=11∘ and ∠RST=130∘ find ∠QRS
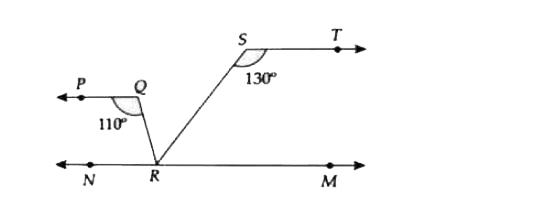
View SolutionIn the given figure, if PQ∣∣ST,∠PQR=110∘ and ∠RST=130∘, then find ∠QRS.
View SolutionIn the following figure , QS=x,SR=y,∠QPR=90∘and∠PSR=90∘, Find the (PQ)2=(PR)2 interms of x and y.

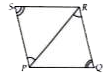
View SolutionIn the given figure, ∠SPR=∠QRPand∠RSP=∠PQR. Prove that PQ = RS.
View Solution