Following is the data showing weights of 40 students in a class . Find its median .
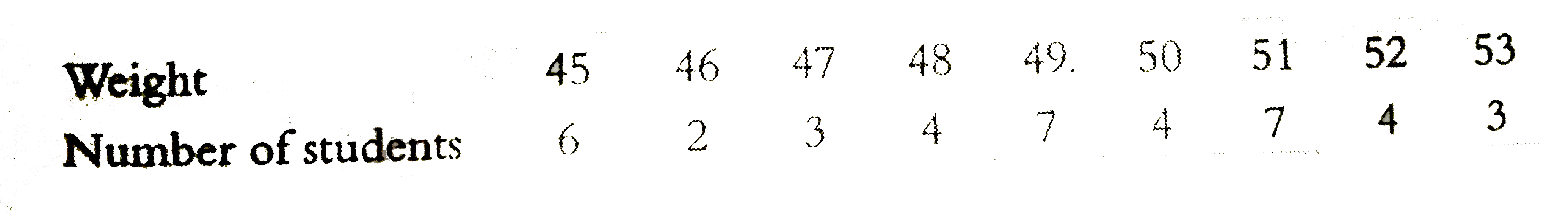
To find the median , we prepare less than cumulative frequency table as given below :

Here , n = 40 which is even .
∴ Median = Value of 402 , or the 20th observation .
From the column of cumulative frequency , the value of 20th observation is 49 .
∴ Median = 49 kg .
Topper's Solved these Questions
- STATISTICS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - STATISTICS EXERCISE - Very short answer type questions
30 Videos
- STATISTICS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - STATISTICS EXERCISE - Short Answer Type Questions
13 Videos
- SHARES AND DIVIDENDSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SHARES AND DIVIDENDSEXERCISE - Level 3
15 Videos
- TAXATION BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - TAXATION EXERCISE - LEVEL 3
10 Videos
Similar Questions
Given below is the data showing heights of 50 students in a class. Find its median.
Height(in cm)162164166167168170173175177180Number of Students64512837221
View SolutionFind the mean weight of 20 students in your class.
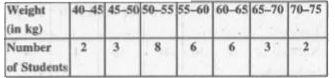
View SolutionThe distribution below gives the weights of 30 students of a class. Find the median weight of the students.
View SolutionFollowing data gives the marks obtained by 100 students in a test. Find the median

View SolutionThe distribution below gives the weights of 30 students of a class. Find the median weight of the students.

View SolutionThe distribution below gives the weight of 30 students in a class. Find the median weight of students: Weight (in kg): 40-45 45-50 50-55 55-60 60-65 65-70 70-75 No. of students: 2 3 8 6 6 3 2
View SolutionA school keeps medical record of all the students. Following table shows the gain in weights by 40 students of Class X in a year. Find the median gain in weight.
View SolutionThe following are the marks of 9 students in a class. Find the median: 34, 32, 48, 38, 24, 30, 27, 21, 35
View SolutionFollowing table shows the weights of 12 students: Find the mean weight.
View SolutionThe weights of 20 students in a class are given below.

Find the median of the above frequency distribution .
View Solution
