Solve the simultaneous equations:
2x-3y = 11 and 5x + 4y =16
x=5,y=−13
x=2,y=23
x=-1, y = 4
x=4,y=−1
The correct Answer is:D
To solve the simultaneous equations 2x−3y=11 and 5x+4y=16, we can use the method of elimination. Here are the steps:
Step 1: Write down the equations
We have the following two equations:
1. 2x−3y=11 (Equation 1)
2. 5x+4y=16 (Equation 2)
Step 2: Make the coefficients of x or y the same
To eliminate x, we can multiply Equation 1 by 5 and Equation 2 by 2:
- Multiply Equation 1 by 5:
5(2x−3y)=5(11)⟹10x−15y=55(Equation 3)
- Multiply Equation 2 by 2:
2(5x+4y)=2(16)⟹10x+8y=32(Equation 4)
Step 3: Subtract the new equations
Now, we can subtract Equation 4 from Equation 3 to eliminate x:
(10x−15y)−(10x+8y)=55−32
This simplifies to:
−15y−8y=23⟹−23y=23
Step 4: Solve for y
Now, divide both sides by -23:
y=23−23=−1
Step 5: Substitute y back into one of the original equations
Now that we have y=−1, we can substitute this value back into Equation 1 to find x:
2x−3(−1)=11
This simplifies to:
2x+3=11
Subtract 3 from both sides:
2x=11−3⟹2x=8
Now divide by 2:
x=82=4
Step 6: Write the final solution
The solution to the simultaneous equations is:
x=4,y=−1
We have the following two equations:
1. 2x−3y=11 (Equation 1)
2. 5x+4y=16 (Equation 2)
To eliminate x, we can multiply Equation 1 by 5 and Equation 2 by 2:
- Multiply Equation 1 by 5:
5(2x−3y)=5(11)⟹10x−15y=55(Equation 3)
- Multiply Equation 2 by 2:
2(5x+4y)=2(16)⟹10x+8y=32(Equation 4)
Now, we can subtract Equation 4 from Equation 3 to eliminate x:
(10x−15y)−(10x+8y)=55−32
This simplifies to:
−15y−8y=23⟹−23y=23
Now, divide both sides by -23:
y=23−23=−1
Now that we have y=−1, we can substitute this value back into Equation 1 to find x:
2x−3(−1)=11
This simplifies to:
2x+3=11
Subtract 3 from both sides:
2x=11−3⟹2x=8
Now divide by 2:
x=82=4
The solution to the simultaneous equations is:
x=4,y=−1
Topper's Solved these Questions
- MATRICESBook:PEARSON IIT JEE FOUNDATIONChapter:MATRICESExercise:EXERCISE CONCEPT APPLICATION (LEVEL 2)
Explore 19 Videos
- MATRICESBook:PEARSON IIT JEE FOUNDATIONChapter:MATRICESExercise:EXERCISE CONCEPT APPLICATION (LEVEL 3)
Explore 15 Videos
- MATRICESBook:PEARSON IIT JEE FOUNDATIONChapter:MATRICESExercise:ESSAY TYPE QUESTIONS
Explore 5 Videos
- MATHEMATICAL INDUCTION AND BIONOMIAL THEOREMBook:PEARSON IIT JEE FOUNDATIONChapter:MATHEMATICAL INDUCTION AND BIONOMIAL THEOREMExercise:LEVEL 3
Explore 15 Videos
- MENSURATIONBook:PEARSON IIT JEE FOUNDATIONChapter:MENSURATIONExercise:Level 3
Explore 21 Videos
Similar Questions
Solve the simultaneous equations: 5x−3y=8,3x+y=2
View SolutionSolve the simultaneous equations: 2x+3y=7,3x−y=5
View SolutionSolve the simultaneous equations: 2x+y=10,3x+4y=25
View SolutionSolve the simultaneous equations: x+11y=1,8x+13y=2
View SolutionSolve the simultaneous equations.
2x−3y=15,8x+5y=77
View SolutionSolve the simultaneous equations: 15x+17y=21,17x+15y=11
View SolutionComplete the following activity to solve the simultaneous equations 5x+3y=−11 and 2x+4y=−10 by Cramer's rule.
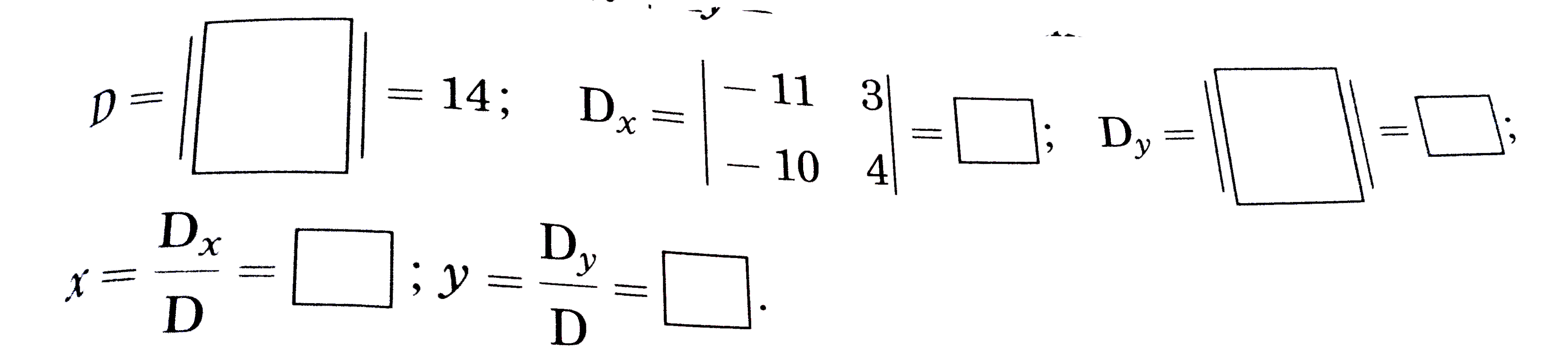
View SolutionSolve the Simultaneous equations
3x−3y=9,2x+y=13
View SolutionSolve the simultaneous equations :
4x+5y=7,3x+4y=5
View SolutionSolve the simultaneous equations: Draw graph of 2x−y=4
View Solution
