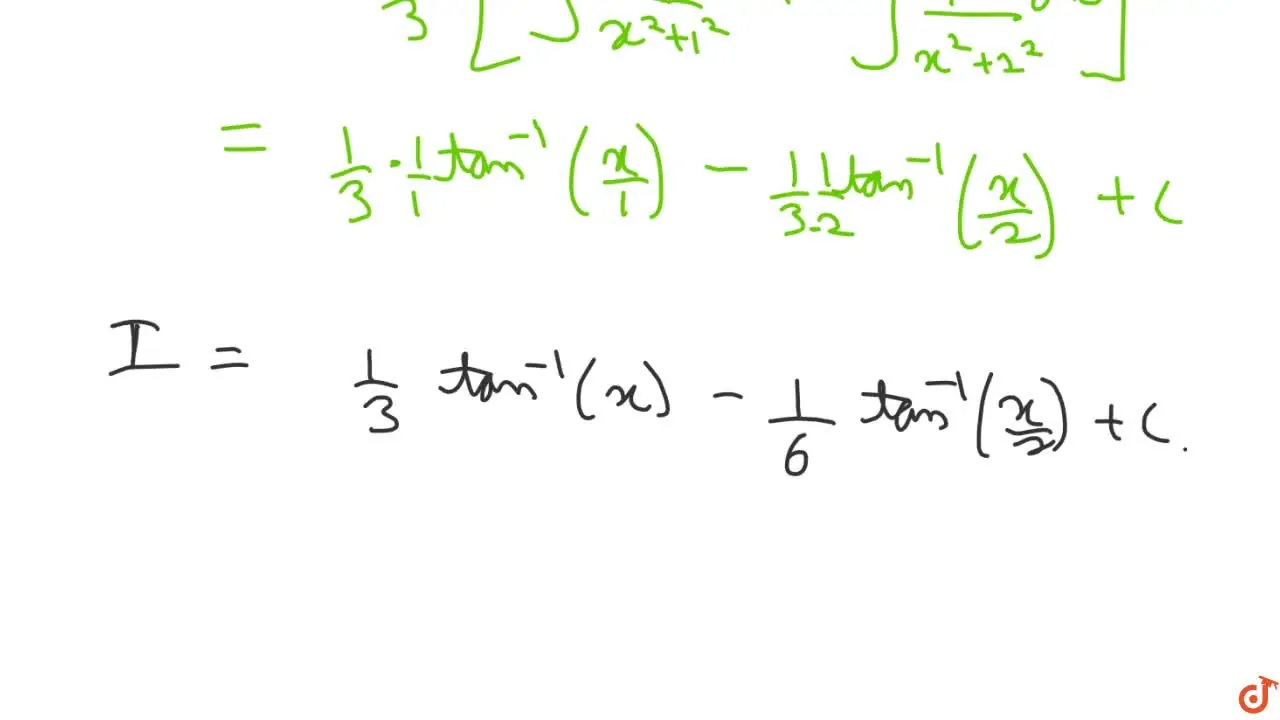Evaluate: ∫1(x2+1)(x2+4) dx
A
tan−1x+12tan−1(x2)+C
B
tan−1x−12tan−1(x2)+C
C
13[tan−1x−12tan−1(x2)]+C
D
13[tan−1x+12tan−1(x2)]+C
Video Solution
Text Solution
The correct Answer is:C
∫1(x2+1)(x2+4)dx
=13∫3(x2+1)(x2+4)dx
=13∫(x2+4)−(x2+1)(x2+1)(x2+4)dx
=13∫1x2+1dx−13∫1x2+4dx
=13[tan−1x−12tan−1(x2)]+C
|
Updated on:21/07/2023
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - INTEGRATIONEXERCISE - Exercise 7.1121videos
INTEGRATION
- BOOK - NAGEEN PRAKASHANCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Miscellaneous Exercise18videos
DIFFERENTIAL EQUATIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )9videos
INVERES TRIGONOMETRIC FUNCTIONS
Similar Questions
Evaluate: ∫1(x2+1)(x2+2) dx
View SolutionEvaluate: ∫1(x+1)2(x2+1) dx
View SolutionEvaluate: ∫5x(x+1)(x2−4) dx
View SolutionEvaluate: ∫1x2√1+x2 dx
View SolutionEvaluate: ∫1x2−x−2dx
View SolutionEvaluate: ∫1(x2+1)(x2+4) dx
View SolutionEvaluate: ∫1x(x−2)(x−4) dx
View SolutionEvaluate: ∫1x3√x2−1 dx
View SolutionEvaluate: ∫1√5−4x−2x2 dx
View SolutionEvaluate: ∫1√x2−4x+2 dx
View Solution