श्रेणीक्रम में L-C-R परिपथ में तात्कालिक विधुत-धारा का व्यंजक प्राप्त करे यदि उस पर प्रत्यावर्ती विधुत वाहक बल आरोपित हो | अनुनाद के लिए शर्त प्राप्त करे | (Derive expression for instantaneous current in a series L-C-R circuit if connected to an alternating emf. Obtain the condition for resonance.)
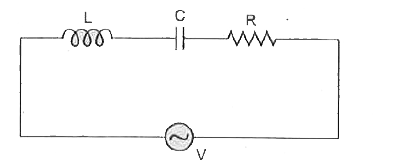
श्रेणीबद्ध L.C.R परिपथ का विश्लेषण - माना श्रेणीबद्ध LCR परिपथ में एक प्रत्यावर्ती स्रोत का प्रयोग किया गया है जिसका वोल्टेज V है, अत:
V=Vmsinωt
परन्तु, V = .L. के परित: विभवांतर +C के परित: विभवांतर +R के परित: विभवांतर
V=Ldidt+qC+iR
Vmsinωt=Ldidt+qC+iR ...(i)
चूँकि i=dqdt
∴ didt=d2qdt2 ...(ii)
समी. (ii) का (i) में प्रयोग करने पर,
Vmsinωt=Ld2qdt2+Rdqdt+qC ...(iii)
समीकरण (iii) अवमंदित दोलक समीकरण के अनुरूप है | माना इस समीकरण का हल निम्नवत है |
q=qmsin(ωt+θ)
∴ dqdt=qmωcos(ωt+θ)
तथा d2qdt2=−qmω2sin(ωt+θ)
समी. (iii) से,
Vmsinωt−qmω[Rcos(ωt+θ)−ωLsin(ωt+θ)+1ωCsinωt+θ]
क्योंकि, ωL=XI तथा, 1ωC=XC
अत:, Vmsinωt=qmω[Rcos(ωt+θ)+(XC−XL)sin(ωt+θ)....] ...(iv)
समी. (v) को z=√R2+(XC−XL)2 से गुणा करने पर,
Vmsinωt=qmωZ[RZcos(ωt+θ)+XC−XLZsinωt+...] ...(v)
यदि RZ=cosθ और, Xe−XLZ=sinϕ ...(vi)
तब, sinϕcosϕ=XC−XLR,tanϕ=XC−XLR
ϕ=tan−1(XC−XLR)
समी. (vi) का (v) में प्रयोग करने पर
Vmsinωt=qmωZ[cosϕcos(ωt+θ)+sinϕ−sin(ωt+θ)] ...(vii)
या, Vmsinwt=qmωZcos(ωt+θ−ϕ)
समी. (vii) के दोनों पक्षों की तुलना करने पर,
Vm=qmwZ
qmω=im
अत: Vm=imZ
तथा, θ−ϕ=−π2
θ=ϕ−π2
परिपथ में धारा,
i=dθdt=ddt[q0sin(ωt+θ)]
i=qmωcos(ωt+θ)
θ को (ϕ−π/2) प्रस्थापित करने पर, 0
i=imsin(ωt+ϕ−π2)
अर्थात, i=imsin(ωt+ϕ)
समी. (viii) में, जब कि ओम के नियमानुसार,
im=VmZ=Vm√R2+(XC−XL)2
विधुतीय अनुनाद-श्रेणी LVR परिपथ - यदि किसी LCR श्रेणी परिपथ में किसी दी गयी आवृति की प्रत्यावर्ती सप्लाई के लिए धांरितीय प्रतिघात तथा प्रेरणिक प्रतिघात का मान बराबर हो तथा परिपथ में प्रवाहित धारा अधिकतम हो तो इस स्थिति को विधुतीय अनुनाद (Electrical Resonance) कहा जाता है | किसी श्रेणी LCR परिपथ में,
धारा I=EZ=E√R2+(Lω−1Cω)2=E√R2+(XC−XL)2
अर्थात यदि परिपथ की प्रतिबाधा (Z) न्यूनतम हो धारा I अधिकतम होती है |
विधुतीय अनुनाद के लिए, (XL−XC)=0 अर्थात XL−XC
या, Lω=1Cω⇒ω2=1LC
ω=1√LC⇒(2πf0)=1√LC
या, अनुनादी आवृति f0=12π√LC
स्पष्ट है कि अनुनादी आवृति का मान परिपथ के प्रतिरोध R पर निर्भर नहीं करता है |
Topper's Solved these Questions
Similar Questions
निम्नलिखित प्रश्नों के उत्तर दीजिए।
निम्न में से किसका मात्रक VOLT−M−1 है ?
View Solutionविद्युत तीव्रता का मात्रक है (The unit of electric intensity is) -
View Solutionएक प्रत्यावर्ती धारा अनुनादी परिपथ में L,C तथा R श्रेणीक्रम में जुड़े हुए है | दोलन परिपथ की आवृत्ति का व्यंजक लिखिये |
View Solutionश्रेणीक्रम में L-C-R परिपथ में विद्युत-धारा के लिए व्यंजक प्राप्त करें यदि उस पर प्रत्यावर्ती विद्युत-वाहक बल अनुप्रयुक्त हो रहा हो | अनुनाद के लिए शर्त प्राप्त करें |
View Solutionश्रेणीक्रम में संयोजित L -C -R प्रत्यावर्ती धारा परिपथ में अनुनाद (resonance ) की स्थिति में
View Solutionएक प्रत्यावर्ती परिपथ में L, C तथा R श्रेणीबद्ध में जुड़े है। अनुनादी आवृति पर :
View Solutionएक प्रत्यावर्ती धारा अनुनादी परिपथ में L,C तथा R श्रेणीक्रम जुड़े है। दोलित परिपथ के आवर्तकाल का व्यजंक लिखिए।
View Solutionविधुत धारा |चालक में विधुत धारा | धारा घनत्व
View Solutionएक प्रत्यावर्ती धारा परिपथ जिसमें L,C और R श्रेणी क्रम में लगे हैं, अनुनाद आवृत्ति पर
View Solutionएकसमान विधुत क्षेत्र में द्विध्रुव पर बल आघूर्ण|OMR|Summary
View Solution12 वी प्री बोर्ड स्पेशल |प्रत्यावर्ती धारा परिपथ के अवयव #!#R-L-C
View Solutionगतिक प्रेरित विधुत वाहक बल
View Solutionविधुत विभव व विधुत क्षेत्र की तीव्रता में संबंद #!#विधुत विभव ,विधुत क्षेत्र पर प्रश्न
View Solutionविभव प्रवणता#!#सेल का विधुत वाहक बल ज्ञात करना
View Solutionसेलो का विधुत वाहक बल #!#टर्मिनल वोल्टता
View SolutionWrite the expression for the impedance of a series L - C - R circuit and then obtain the condition for resonance in the circuit. Find an expression for the resonant frequency.
View Solution
