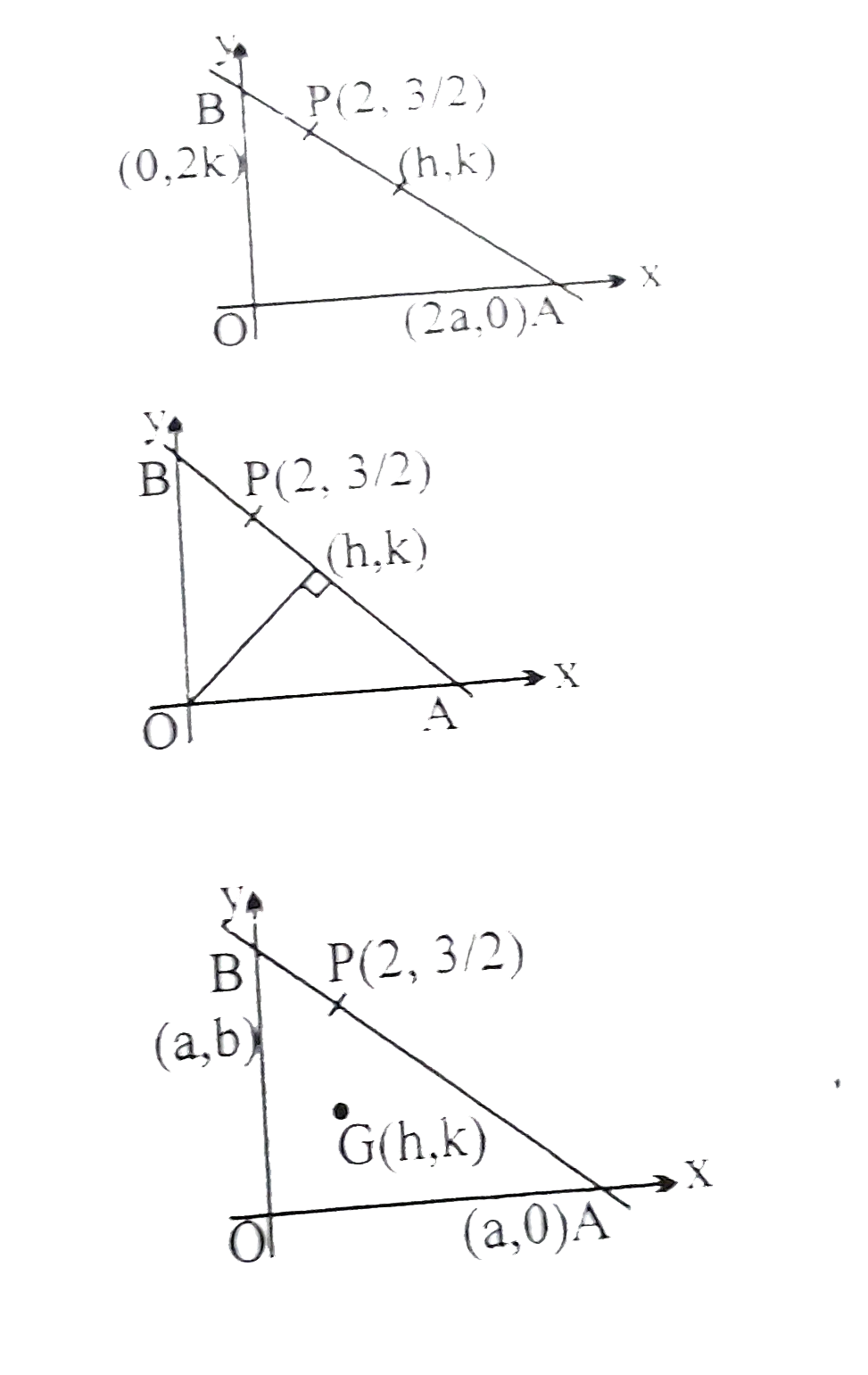
Consider a variable line $L$ which passes through the point of intersection $P$ of the lines $3 x + 4 y = 12$ and $x + 2 y - 5 = 0$ meeting the coordinate axes at points $A$ and $B .$ Then

A

$3 x + 4 y = 4 x y$

B

$3 x + 4 y = 3 x y$

C

$4 x + 3 y = 4 x y$

D

$4 x + 3 y = 3 x y$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Point of intersection of the line
$3 x + 4 y - 12 = 0$
$x + 2 y - 5 = 0$
is $x = 2 and y = 3 / 2$
(i) Equation of AB is
$\frac{x}{2 h} + \frac{y}{2 k} = 1$
$\frac{2}{2 h} + \frac{3}{4 k} = 1$
$∴ 4 k + 3 h = 4 k h \Rightarrow 3 x + 4 y - 4 x y = 0$ Ans.

(ii) $\frac{k}{h} . \frac{k - (3 / 2)}{h - 2} = - 1$
$\frac{k}{h} . \frac{2 k - 3}{h - 2} = - 2$
$2 h (h - 2) + k (2 k - 3) = 0$
$2 (x^{2} + y^{2}) - 4 x - 3 y = 0$ Ans.
Here, $a = 3 h and b = 3 k$
$∴ equation of AB is$
$\frac{x}{3 h} + \frac{y}{3 k} = 1$
$\frac{2}{3 h} + \frac{1}{2 k} = 1$
$3 x + 4 y - 6 x y = 0$ Ans.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A variable line passes through the point of intersection of the lines $x + 2 y - 1 = 0$ and $2 x - y - 1 = 0$ and meets the coordinate axes in A and B. The locus of the mid poind of AB is
A $x + 3 y = 0$
B $x + 3 y = 10$
C $x + 3 y = 10 x y$
Dnone
Question 2 - Select One
If a circle passes through the points where the lines $3 λ x - 2 y - 1 = 0$ and $4 x - 3 y + 2 = 0$ meet the coordinate axes then $λ =$
A $- 1$
B $- 1 / 2$
C $1 / 2$
D1
Question 3 - Select One
A variable straight line drawn through the point of intersection of lines $\frac{x}{a} + \frac{y}{b} = 1$ and $\frac{x}{b} + \frac{y}{a} = 1$ meets the co ordinates axes in A and B. Locus of the mid point of AB is ……….
A2xy (a + b) = ab (x + y)
B2xy (a - b) = ab (x - y)
C2xy (a + b) = ab (x - y)
DNone of the above

BANSAL-TEST PAPERS-Mathematics SECTION-3 (PART-A) [COMPREHENSION TYPE]

Home
Ask Doubt
Profile