The set of angles between 0 and 2π satisfying the equation 4cos2θ−2√2cosθ−1=0 is
{π12,5π12,19π12,23π12}
{π12,7π12,17π12,23π12}
{5π12,13π12,19π12}
{π12,7π12,1712,23π12}
The correct Answer is:B
Step by step video, text & image solution for The set of angles between 0 and 2pi satisfying the equation 4cos^2theta-2sqrt2costheta-1=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Math
15 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS
60 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY
133 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Video
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
Knowledge Check
The value of θ lying between 0 and π2 and satisfying the equation
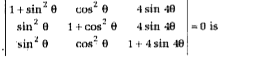 A7π24or11π24B5π24C3π24Dnone of these
A7π24or11π24B5π24C3π24Dnone of theseThe smallest positive angle which satisfies the equation 2sin2θ+√3cosθ+1=0 is 5π6 b. 2π3 c. π3 d. π6
A5π6Bπ6C7π6Dnone of these
The value of theta lying between 0 and π2 and satisfying the equation ∣∣ ∣ ∣∣1+cos2θsin2θ4sin4θcos2θ1+sin2θ4sin4θcos2θsin2θ1+4sin4θ∣∣ ∣ ∣∣=0 is (are) (A) 7π24 (B) 3π8 (C) 11π24 (D) 7π12
View SolutionThe value of θ lying between 0 and π2 and satisfying the equation ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0 (A) 7π24or11π24 (B) 5π24 (C) π24 (D) none
View SolutionThere exists a value of θ between 0 and 2π that satisfies the equation sin4θ−2sin2θ−1=0
View SolutionFind all values of θ lying between 0 and 2π satisfying the equation rsinθ=√3 and r+4sinθ=2(√3+1)
View SolutionFind the acute angle θ satisfying the equation 2sin2θ−2√2sinθ+1=0.
View SolutionThere exist a value of θ between 0 and 2π that satisfies the equaition sin4θ−2sin2θ+1=0
View Solution