Find the intervals in which the following functions are strictly increasing or decreasing: (a x2+2x−5 (b) 10−6x−2x2 (c) −2x3−9x2−12x+1 (d) 6−9x−x2 (e) (x+1)3(x−3)3

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

(a) f(x)=x2+2x+5
f'(x)=2x+2
Letf'(x)=0
ocr_image
⇒2x+2=0
⇒x=−1
ocr_image
∴F(x) is strictly decreasing in (−∞,−1) and strictly increasing in (=1,∞).
(b) f(x)=10−6x−2x2
⇒f'(x)=−6−4x
Let f'(x)=0
⇒−6−4x=0
⇒x=−32
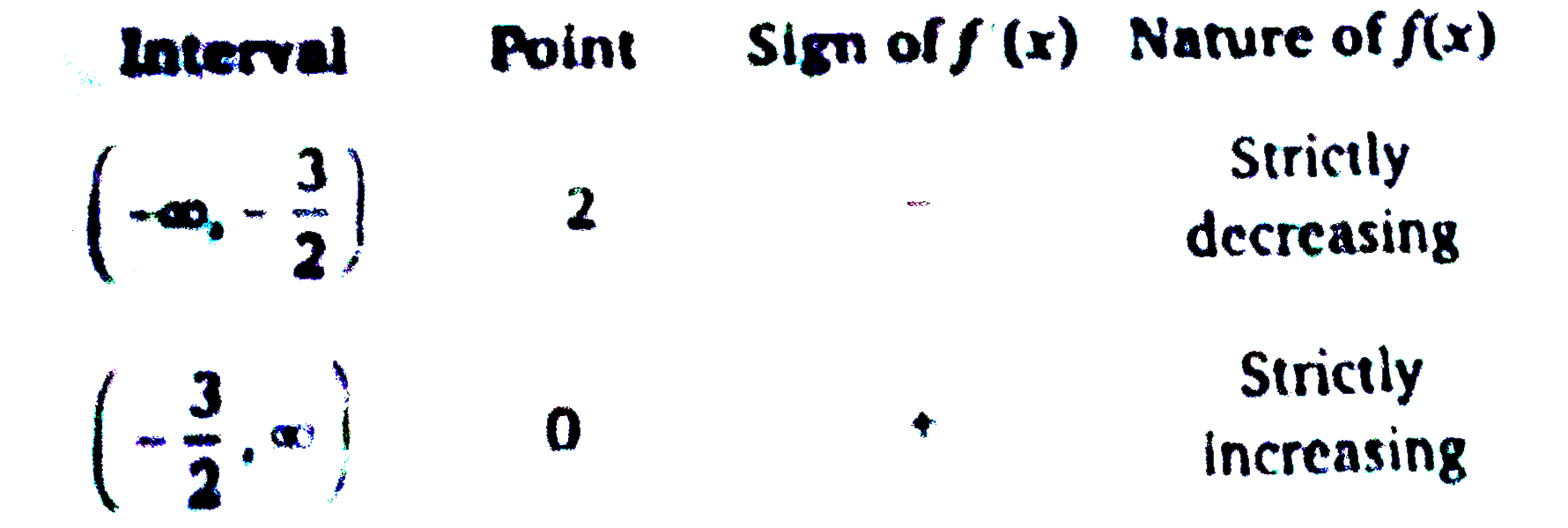
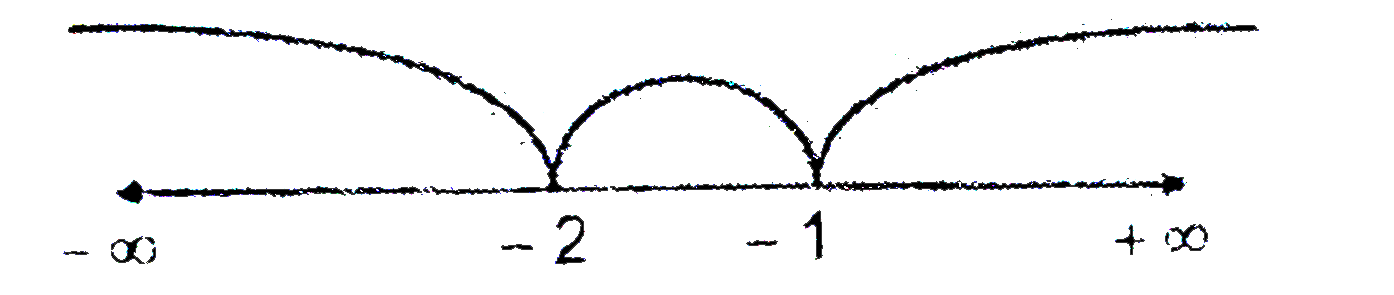
ocr_image
ocr_image
∴f(x) is strictly decreasing in (−∞,−32) and strictly increasing in (−32,∞).
(c) f(x)=−2x3−9x2−12x−1
⇒f'(x)=−6x2−18x−12
=−6(x2+3x+2)
=−6(x+1)(x+2)
ocr_image
Let f'(x)=0
⇒−6(x+1)(x+2)=0
⇒x+1=0orx+2=0
⇒x=−1orx=−2
ocr_image
∴f(x) is strictly decreasing in (−2,−1) and atrictly increasing in (−∞,−2)∪(−1,∞).
(d) f(x)=6−9x−x2
Let f'(x)=0
⇒−9−2x=0
⇒x=−92
∴f(x),is strictly decreasing in (−∞,−92) and strictly increasing in(−92,∞).
(e) f(x)=(x+1)3(x−3)3
⇒f'(x)=(x+1)3⋅3(x−3)2+(x−3)3⋅3(x+1)2
=3(x+1)2(x−3)2(x+1+x−3)
=6(x+1)2(x−3)2(x−1)
If f'(x)>0
then 6(x+1)2(x−3)2(x−1)>0,x≠−1,x≠3
⇒x−1>0
⇒x>1
∴f(x) is strictly increasing in the interval (1,∞)−{3}.
Again f'(x)<0
⇒3(x+1)2(x−3)2)(x−1)<0x≠−1,x≠3
⇒x−1<0
⇒x<1
∴f(x) is strictly decreasing in the interval (−∞,1)−{−1}.

Updated on:21/07/2023
|
Class 12MATHSAPPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions