An open tank of square base is to be constructed which has a given quantity of water. Prove that for least material used for the construction of tank, the depth will be half of the width of tank.
To solve the problem of finding the depth of an open tank with a square base that minimizes the material used while containing a fixed volume of water, we can follow these steps:
Step 1: Define Variables
Let:
- A = side length of the square base of the tank
- d = depth of the tank
- V = fixed volume of water in the tank
Step 2: Write the Volume Equation
The volume V of the tank can be expressed as:
V=A2⋅d
Since the volume is fixed, we can express d in terms of A:
d=VA2
Step 3: Write the Surface Area Equation
The surface area S of the open tank (which includes the base and the four sides) is given by:
S=A2+4⋅(A⋅d)
Substituting d from the volume equation into the surface area equation gives:
S=A2+4A(VA2)
This simplifies to:
S=A2+4VA
Step 4: Differentiate the Surface Area
To find the minimum surface area, we differentiate S with respect to A:
dSdA=2A−4VA2
Step 5: Set the Derivative to Zero
Setting the derivative equal to zero to find critical points:
2A−4VA2=0
Rearranging gives:
2A3=4V
Thus:
A3=2V⇒A=(2V)1/3
Step 6: Substitute Back to Find Depth
Now substituting A back into the equation for d:
d=VA2=V((2V)1/3)2=V(2V)2/3=V1/322/3
This can be simplified to:
d=12⋅(2V)1/3
Step 7: Relate Depth to Width
From the expression for A:
A=(2V)1/3
Thus, we can relate d to A:
d=12A
Conclusion
We have shown that for the least material used in the construction of the tank, the depth d is half of the width (or side length A) of the tank:
d=12A
Let:
- A = side length of the square base of the tank
- d = depth of the tank
- V = fixed volume of water in the tank
The volume V of the tank can be expressed as:
V=A2⋅d
Since the volume is fixed, we can express d in terms of A:
d=VA2
The surface area S of the open tank (which includes the base and the four sides) is given by:
S=A2+4⋅(A⋅d)
Substituting d from the volume equation into the surface area equation gives:
S=A2+4A(VA2)
This simplifies to:
S=A2+4VA
To find the minimum surface area, we differentiate S with respect to A:
dSdA=2A−4VA2
Setting the derivative equal to zero to find critical points:
2A−4VA2=0
Rearranging gives:
2A3=4V
Thus:
A3=2V⇒A=(2V)1/3
Now substituting A back into the equation for d:
d=VA2=V((2V)1/3)2=V(2V)2/3=V1/322/3
This can be simplified to:
d=12⋅(2V)1/3
From the expression for A:
A=(2V)1/3
Thus, we can relate d to A:
d=12A
We have shown that for the least material used in the construction of the tank, the depth d is half of the width (or side length A) of the tank:
d=12A
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 6h (multiple Choice Questions)
Explore 10 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 6i (multiple Choice Questions)
Explore 10 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 6f
Explore 19 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Miscellaneous Exercise
Explore 19 Videos
Similar Questions
An open tank with a square base and vertical sides is to be constructed form a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when depth of tank is half its width. If the cost is to be borne by nearby settled lower income families, for whom water will be provided, what kind of value is hidden in the question
View SolutionAn open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of the material will be least when depth of the tank is half of its width.
View Solution
Knowledge Check
A tank with vertical walls is mounted so that its base is at a height H above the horizontal ground. The tak is filled with water to a depth h. A hole is puched in the side wall of the tank at a depth x below the water surface. To have maximum range of the emerging stream, the value of x is
AH+h4BH+h2CH+h3D3(H+h)4
An open tank is to be constructed with square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead will be least, if depth is made half of width.
View SolutionAn open tank is to be constructed with square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead will be least, if depth is made half of width.
View SolutionA water tank is supported by four pillars. The pillars are strong enough to sustain ten times the stress developed in them when the tank is completely full. An engineer decides to increase the every dimension of the tank and the pillars by hundred times so as to store more water. Do you think he has taken a right decision? Assume that material used in construction of the tank and pillars remain same.

View SolutionIf one-third of a tank holds 80 litres of water, then the quantity of water that half of the tank holds is
View SolutionAn open cylindrical tank whose base is a circle is to be constructed of metal sheet so as to contain a volume of πa3cu.cm of water.Find the dimensions so that the quantity of metal sheet required is a minimum.
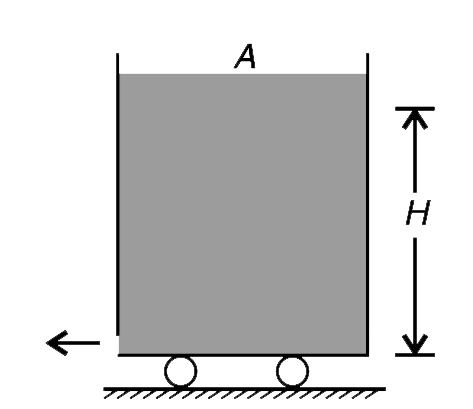
View SolutionAn open tank of cross sectional area A contains water up to height H. It is kept on a smooth horizontal surface. A small orifice of area A0 is punched at the bottom of the wall of the tank. Water begins to drainout. Mass of the empty tank may be neglected.
(i) Prove that the tank will move with a constant acceleration till it is emptied. Find this acceleration.
(iii) Find the find speed acquired by the tank when it is completely empty.
View SolutionA leak can empty a completely filled tank in 15 hours. If the tank is full of water and a tap is opened which fills 4 litres of water per minute in the tank. The leak now takes 30 hours to empty the tank, then find the capacity of tank.
View Solution

