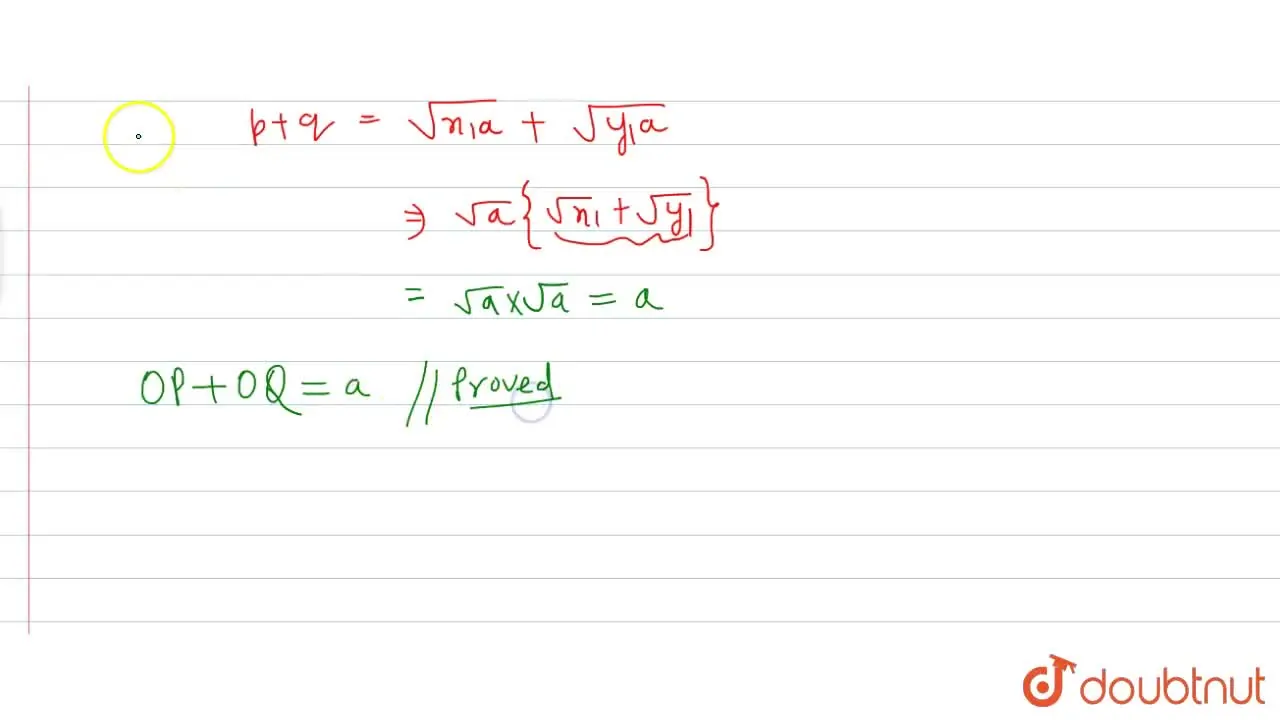The tangent drawn at any point of the curve √x+√y=√a meets the OX and OY axes at points P and Q respectively, prove that OP+OQ = a.
Step by step video, text & image solution for The tangent drawn at any point of the curve sqrtx+sqrty = sqrta meets the OX and OY axes at points P and Q respectively, prove that OP+OQ = a. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6e16videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6f19videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6c19videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
Similar Questions
Let a tangent be drawn at a point on the focus f(x,y) = 0 and it meets the positive X and Y- axes at point P and Q. Let A and G be respectively the arithmetic and geometric means of the segments OP and OQ. Now,
If G = 1 then, the locus f(x,y)=0, isView SolutionA normal is drawn at a point A (x, y) of a curve. It meets the X -axis and Y - axis at point P and Q respectively such that 1OP+1OQ=1 where O is the origin. Then, the equation of such a curve passing through (5, 4) is
View SolutionThe point on the curve √x+√y=√a at which the normal is parallel to the X-axis, is
View SolutionThe tangent at any point on the curve x=acos3θ,y=asin3θ meets the axes in PandQ . Prove that the locus of the midpoint of PQ is a circle.
View SolutionIf the tangent drawn at any point P(acos4θ,asin4θ) on the curve √x+√y=√a meets the co-ordinate axes in A , B respectively then. The value of PA when θ=π4 is (where PA is the length of tangent P)
View SolutionIf the tangent drawn at any point P(acos4θ,asin4θ) on the curve √x+√y=√a meets the co-ordinate axes in A and B respectively then
Q: The value of OA−OBOA+OB is (where O is origin)View SolutionThe length of sub-tangent to the curve √x+√y=3 at the point (4,1) is
View SolutionFrom vertex O ofthe parabola y2=4ax perpendicular is drawn at a tangent to the parabola. If it meets the tangent and the parabola at point P and Q respectively then OP.OQ is equal to (A) constant (B) 1 (C) -1 (D) 2
View SolutionIf the tangent at the point (p,q) to the curve x3+y2=k meets the curve again at the point (a, b), then
View SolutionWhat is the area bounded by the curve √x+√y=√a(x,y≥0) and the corrdinate axes?
View Solution