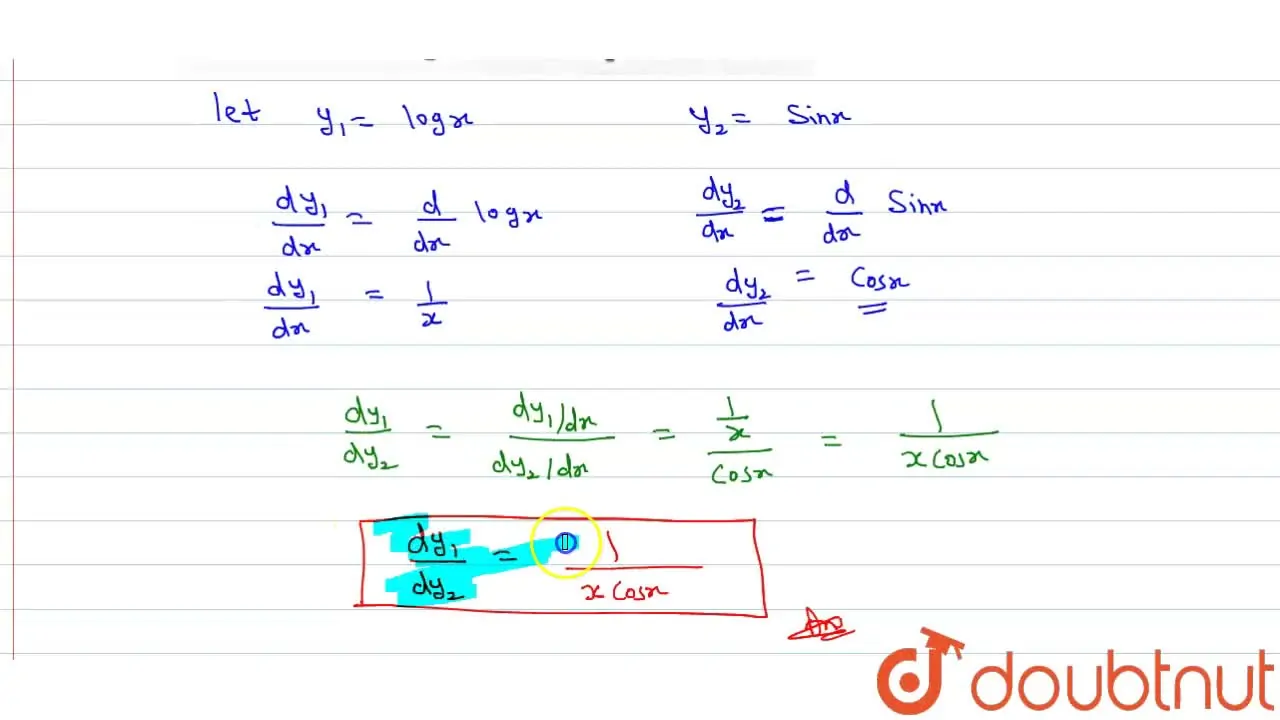
Differentiate log x with respect to sin x
Video Solution
Text Solution
The correct Answer is:1xcotx
|
Answer
Step by step video, text & image solution for Differentiate log x with respect to sin x by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5l18videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5m19videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5j14videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHANCHAPTER - DETERMINANTSEXERCISE - Miscellaneous Exercise19videos
DETERMINANTS
Similar Questions
Differentiate logx with respect to cot x.
View SolutionDifferentiate logsinx with respect to x :
View SolutionDifferentiate logsinx with respect to√cosx .
View SolutionDifferentiate logsinx with respect to √cosx .
View SolutionDifferentiate (log x) with repect to tan x.
View SolutionDifferentiate log(sin x) with respect to x
View SolutionDifferentiate sin(logx) with respect to x :
View SolutionDifferentiate exlogx with respect to x :
View SolutionDifferentiate log sin x3with respect to 'x'
View SolutionDifferentiate (logx)x with respect to logx .
View Solution