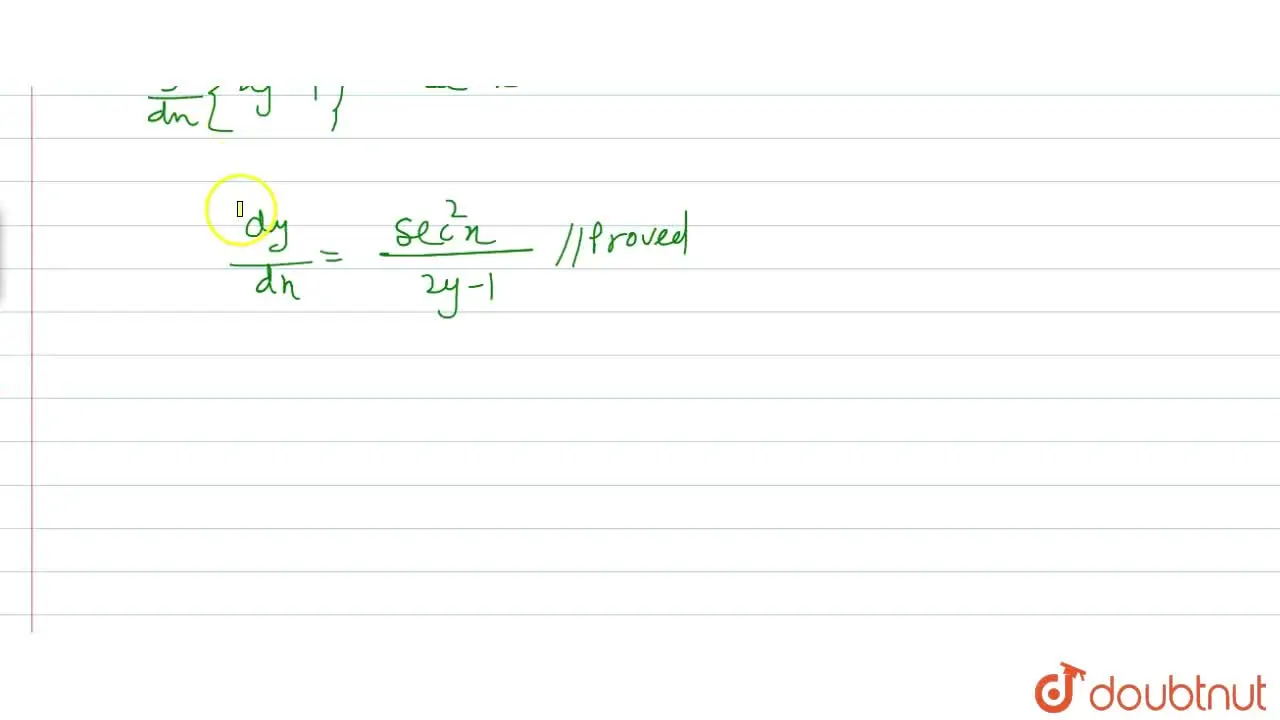Ify=√tanx+√tanx+√tanx+....∞ then prove that dydx=sec2x2y−1.
Step by step video, text & image solution for If y=sqrt(tan x+sqrt(tan x +sqrt(tan x+....oo))) " then prove that " dy/dx = sec^2 x /(2y-1). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5j14videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5k12videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5h26videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHANCHAPTER - DETERMINANTSEXERCISE - Miscellaneous Exercise19videos
DETERMINANTS
Similar Questions
Ify=√sinx+√sinx+√sinx+....∞ then prove that dydx=cosx2y−1.
View SolutionIfy=√cosx+√cosx+√cosx+....∞ then prove that dydx=sinx1−2y.
View SolutionIf y=√tanx+√tanx+√tanx+...+∞, then prove that (2y−1) dydx−sec2x=0.
View SolutionIfy=√logx+√logx+√logx+....∞ then prove that dydx=1x(2y−1).
View SolutionIf y=√tanx+√tanx+√tanx+ .−−→ ∞ , prove that dydx=sec2x2y−1
View SolutionIf y=√cosx+√cosx+√cosx+......∞, then prove that dydx=sinx1−2y
View SolutionIf y=√tanx+√tanx+√tan+... to ∞, then dydx=
View SolutionIf y=√x+√y+√x+√y+...∞ then prove that dydx=y2−x2y3−2xy−1
View SolutionIf y=√x+√x+√+…..∞ then prove that (2y−1)dydx=1.
View SolutionIf y=√x+√y+√x+√y+∞,thenprovethatdydx=y2−x2y3−2xy−1
View Solution