A point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:

A

a circle

B

an ellipse

C

a hyperbola

D

a pair of lines

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C, D

Let the two sides of the rectangle lie along x-axis and y-axis.
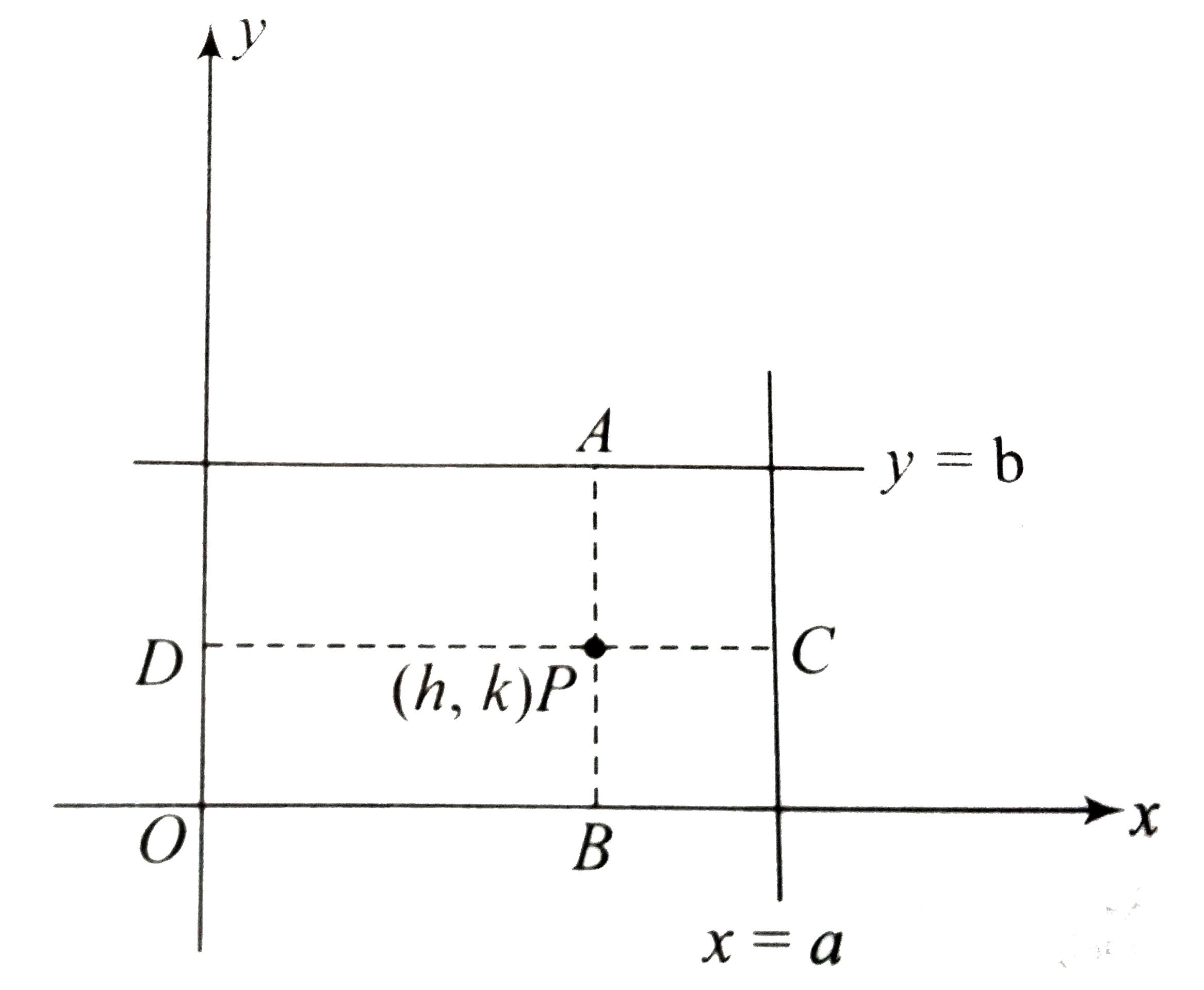
ocr_image
Let point P be (h,k)
Given that
(PA)2+(PB)2=2(PC2+PD2)
⇒k2−(k−b)6(2)=2(h2+(a−h)2)
⇒2k2−2kb+b2=4h2−4ah+2a2
Replacing h by x and k by y
⇒2y2−2by+b2=4x2−4ax+2a2
or 2(y2−by)+b2=4(x2−ax)+2a2
or 4(x−a2)2−2(y−b2)2=b22−a2
Hence it is a hyperbola if b22−a2≠0
or pair of lines if b22−a∘=0

Updated on:21/07/2023
|
Class 12MATHSCONIC SECTIONS

Similar Questions

Knowledge Check

  • Locus of a point which moves such that sum of the squares of its distances from the sides of a square of side unity is 9, is

    Astraight line
    Bcircle
    Cparabola
    Dnone

  • A point moves so that the sum of squares of its distances from the points (1,2) and (-2,1) is always 6. then its locus is

    Athe straight line y−32=−3(x+12)
    Bthe circle with centre (−12,32) and radius 1√2
    Ca parabola with focus (1,2) and directrix passing through (-2,1)
    Dan ellipspe with foci (1,2) and (-2,1)

  • In triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then

    Alocus of P is an ellipse with eccentricity √23
    Blocus of P is a hyperbola with eccentricity √32
    Carea of the quadr5ilateral ABCD=163 sq. units
    Darea of the quadrilateral ABCD=323 sq. units