Question

Let $S$ is the focus of the parabola $y^2=4ax$ and $X$ the foot of the directrix, $PP\text{'}$ is a double ordinate of the curve and $PX$ meets the curve again in $Q.$ Prove that $P\text{'}Q$ passes through focus.

Options

A. line
B. circle
C. parabola
D. none of these

Answer

A

Explanation

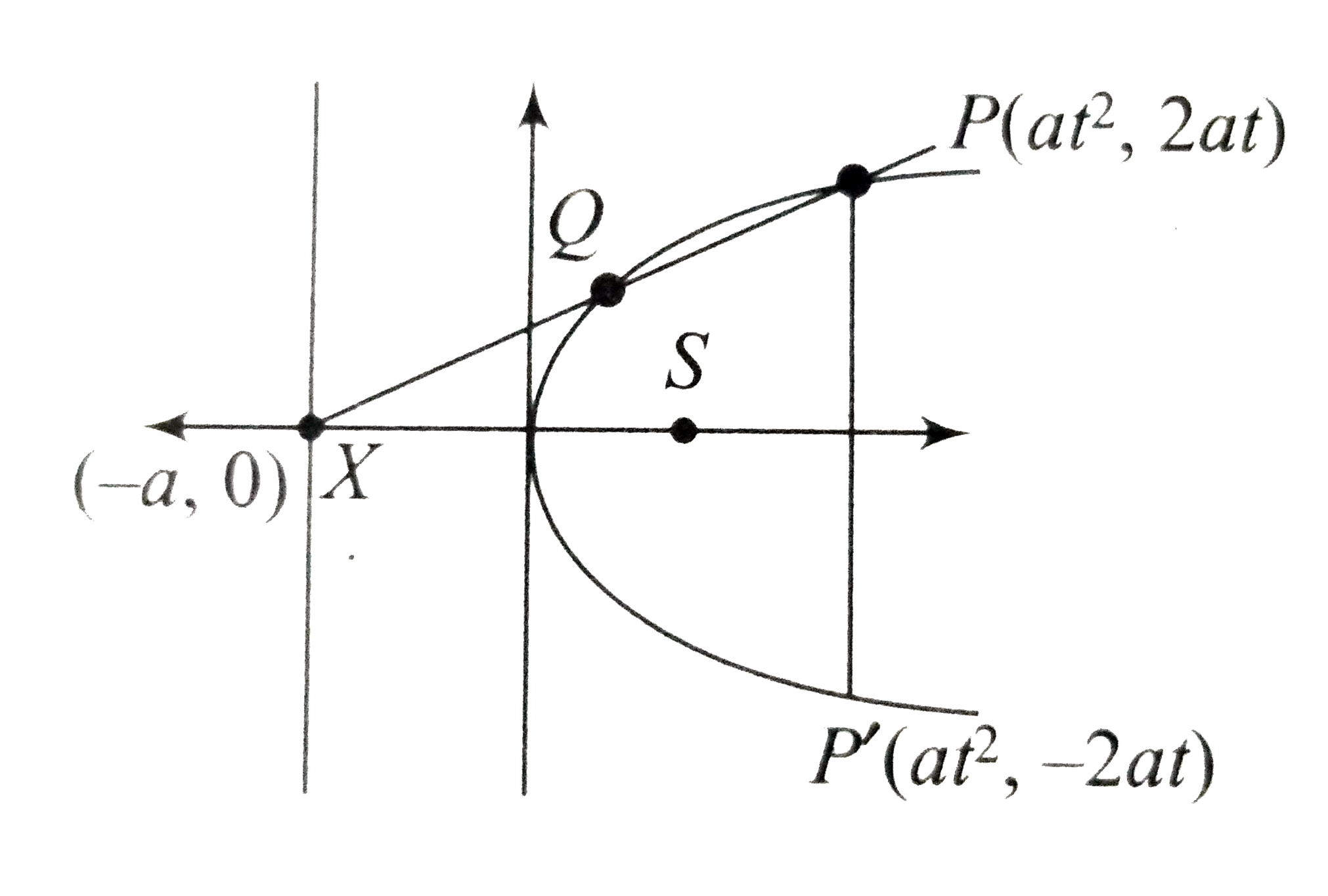
`X: (-a,0)`
`PX: y = (2at-0)/(at^(2) +a) (x+a)`
or `(1+t^(2))y = 2t (x+a)`
Solving with parabola `y^(2) =4ax`, we get
`(4t^(2)(x+a)^(2))/((1+t^(2))^(2)) =4ax`
or `t^(2) (x+a)^(2) = ax (1+t^(2))^(2)`
or `t^(2) x^(2) -(a+at^(4)) x+ at^(2) =0`
or `xt^(2) (x-at^(2)) -a (x-at^(2)) =0`
or `x = (a)/(t^(2))`
`:. Q: ((a)/(t^(2)),(2a)/(t))`
Thus `P' (at^(2)-2at)` and `Q ((a)/(t^(2)),(2a)/(t))`, are extremities of focal chord.
So, tangents at P' and Q intersect on directrix.